3  Cartes univariées

3.1 Cartes de Shewart

On va construire deux graphiques : une carte dite de position et une carte de dispersion. Ces cartes sont appelées les cartes de Shewart.

Exemple

Suivi de production journalière de steacks hachés surgelés durant 12h de production. Chaque heure on prélève 5 steaks et on les pèse.

Les données sont disponibles ici

X weight.1 weight.2 weight.3 weight.4 weight.5
1 98.6 100.3 100.9 100.2 99.6
2 100.3 99.5 98.9 100.2 100.6
3 99.2 98.8 101.5 100.3 101.0
4 101.1 97.8 98.9 101.3 101.7
5 101.0 99.8 97.3 99.4 100.8
6 101.1 100.1 99.0 100.7 99.9

On va construire les cartes de contrôle données ci-dessous

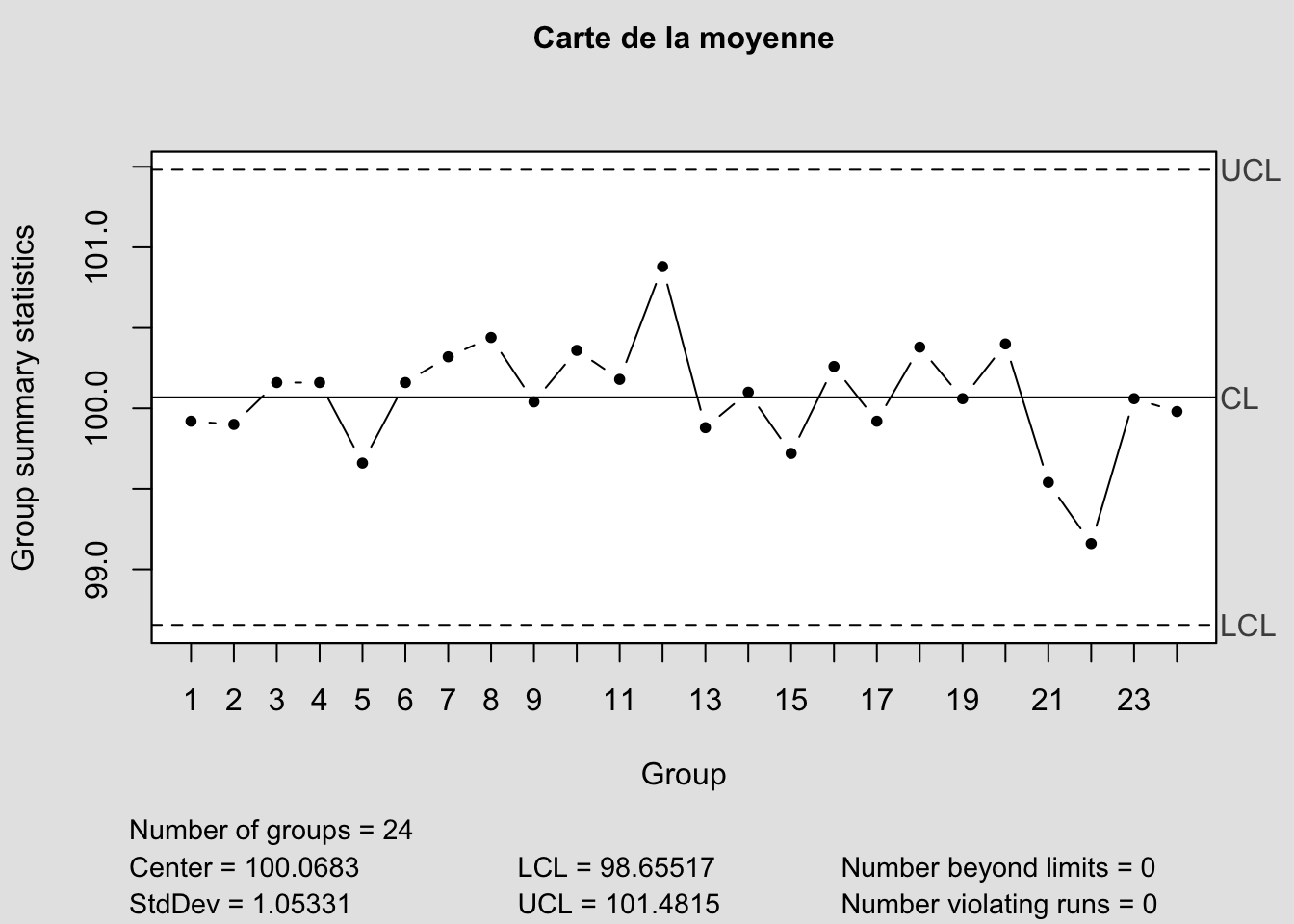
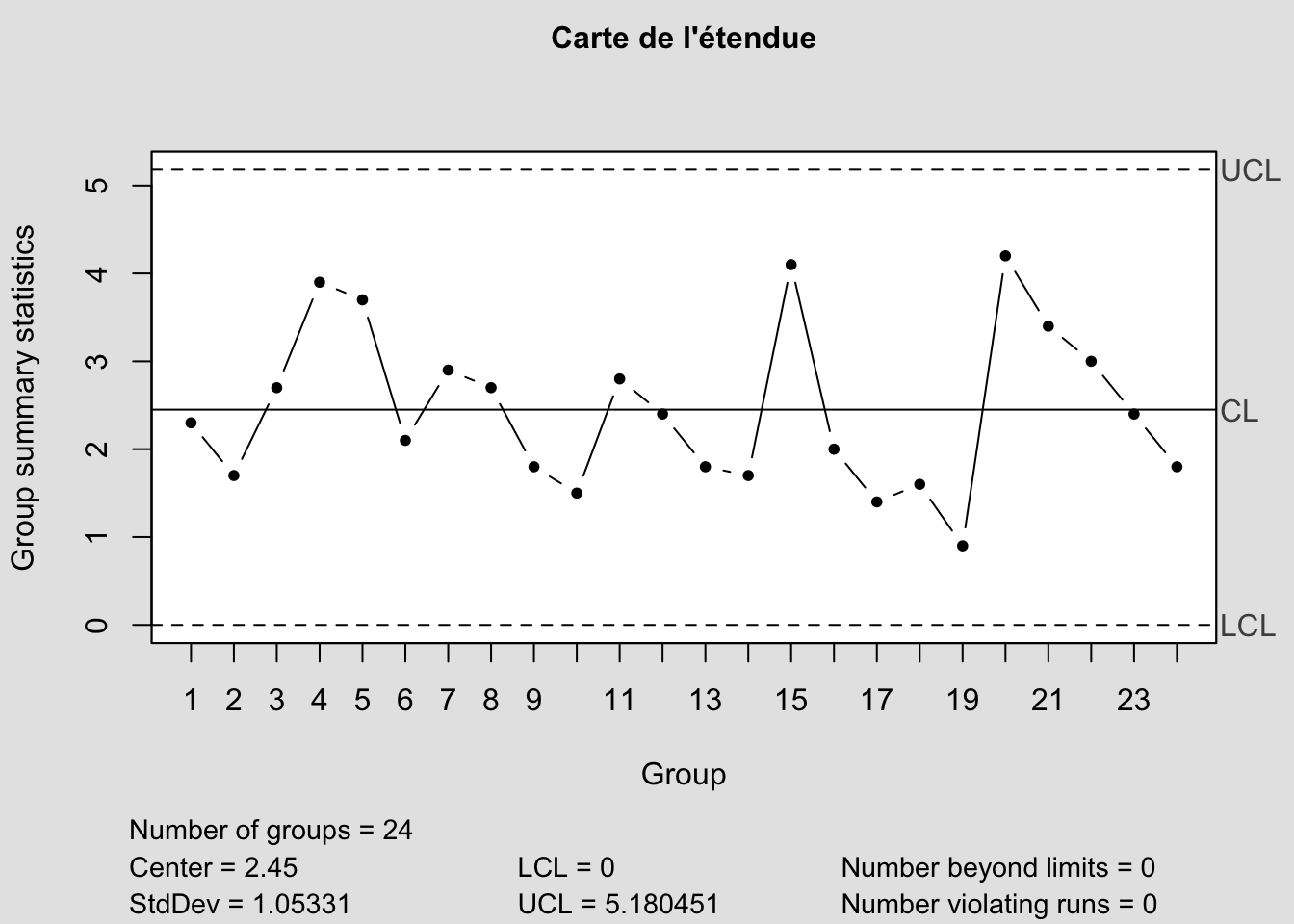
Pour chaque échantillon de 5 steacks on calcule la moyenne et l’écart type et on les reporte sur les cartes correspondantes.

3.1.1 Distribution des paramètres

On suppose que tous les paramètres suivent une loi normale.

  • La moyenne d’un échantillon \(\bar Y \sim \mathcal N(\mu,\frac{\sigma}{\sqrt n}).\)

  • L’étendue d’un échantillon \(R \sim \mathcal N(\mu_R,\sigma_R).\)

  • L’écart type d’un échantillon \(S \sim \mathcal N(\mu_S,\sigma_S).\)

On définit alors les limites de surveillance et de contrôle pour chaque carte. Pour la carte de la moyenne :

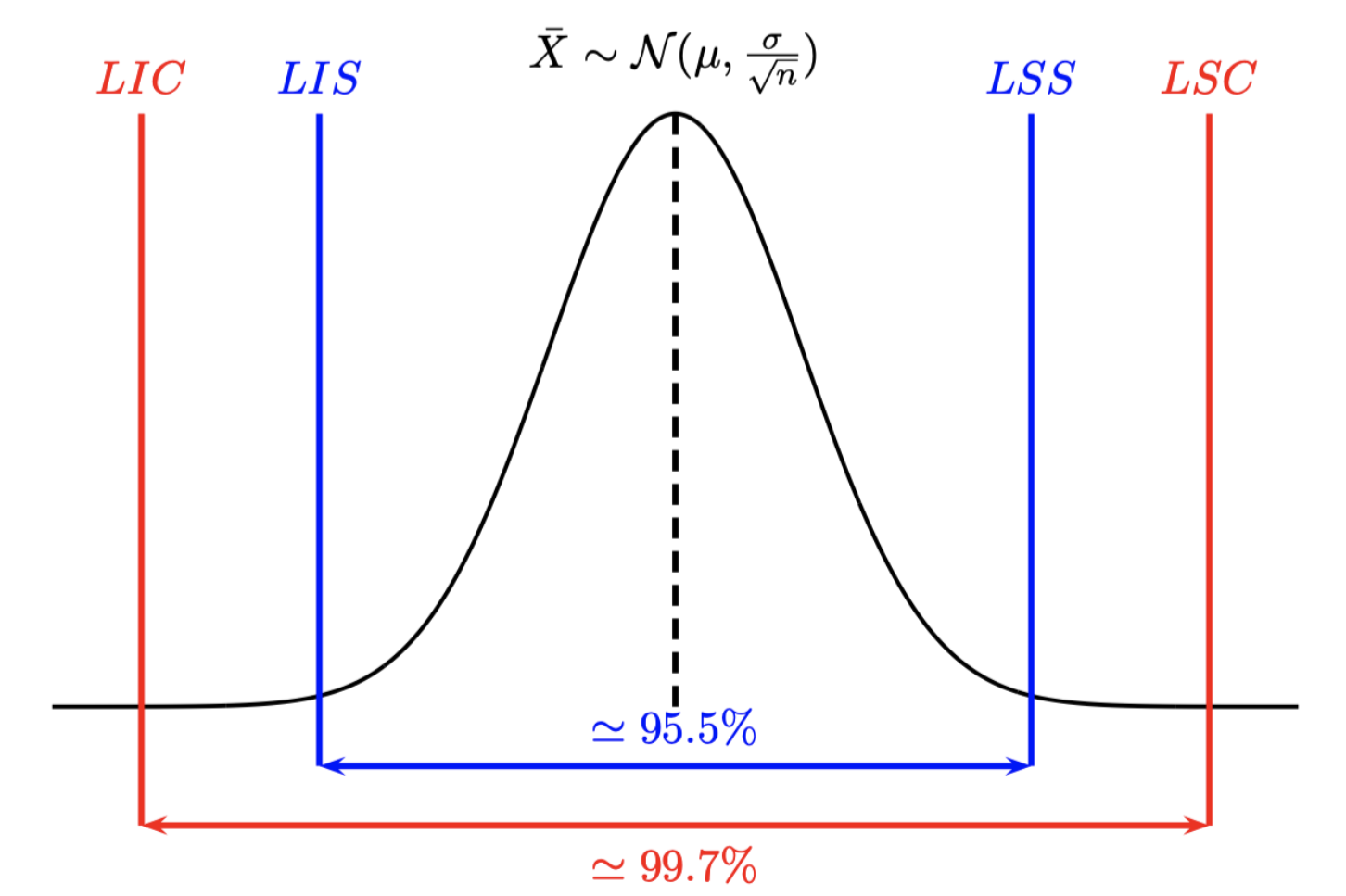On se fixe un risque \(\alpha\) de stoper la production alors que celle-ci est sous contrôle (Fausses alertes). On cherche donc un intervalle de confiance \(1-\alpha\) de \(\bar X\) La distribution des moyennes étant normale on a

\[ \begin{cases} LI=\mu-z_{1-\alpha/2}\frac{\sigma}{\sqrt n} \\ LS=\mu+z_{1-\alpha/2}\frac{\sigma}{\sqrt n} \\ \mathbb P(LI<\bar X<LS)=1-\alpha \end{cases} \]

On pourra en conclure que la moyenne \(\bar X\) de l’échantillon considéré n’est pas significativement différente de la moyenne \(\mu\) (c’est à dire que le procédé est sous contrôle) si \(\bar X \in [LI,LS].\)

Les limites de surveillance sont définies de façon à déterminer, au risque de 4.5%, les moyennes significativement différentes de la moyenne globale :

  • Limite inférieure de surveillance (LIS): \(LIS=\mu-2\frac{\sigma}{\sqrt n}\)

  • Limite supérieure de surveillance (LSS): \(LSS=\mu+2\frac{\sigma}{\sqrt n}\)

Les limites de contrôle sont définies de façon à déterminer, au risque de 0.3% de fausses alertes, les moyennes significativement différentes de la moyenne globale :

  • Limite inférieure de contrôle (LIC): \(LIC=\mu-3\frac{\sigma}{\sqrt n}\)

  • Limite supérieure de contrôle (LSC): \(LSC=\mu+3\frac{\sigma}{\sqrt n}\)

Limites des cartes de contrôle

On a prélevé à intervalles réguliers \(k\) échantillons de \(n\) observations. On a calculé \(\bar y_j,R_j\) la moyenne et l’étendue de chacun des \(k\) échantillons.

Pour construire :

  • La carte de la moyenne on utilise \(\hat \mu_I=\frac 1{k} \displaystyle\sum_{j=1}^k \bar y_{j}\) et \(\hat \sigma_I = \dfrac{\bar R}{d_2}\).

  • La carte de l’étendue on utilise \(\hat\mu_R=\bar R\) et \(\hat \sigma_R=\frac{d_3}{d_2}\bar R\).

  • La carte de l’écart type on utilise \(\hat\mu_S=\bar S\) et \(\hat \sigma_S=\frac{\sqrt{1-c_4^2}}{c_4}\bar S\).

3.1.2 Retour sur l’exemple :

  1. Calculer les limites de contrôles des cartes de la moyenne et de l’écart type.

  2. Construire les cartes s’obtiennent en utilisant la fonction plot_chart() du package multiSPC.

Voir la correction 
df<-data[,-1]
n=ncol(df)
M=apply(df,1,mean)
S=apply(df,1,sd)
mu=mean(M)
sigI=mean(S)/c4(n)
LICm=mu-3*sigI/sqrt(n)
LSCm=mu+3*sigI/sqrt(n)
LICs=mean(S)-3*mean(S)*sqrt(1-c4(n)^2)/c4(n)
LSCs=mean(S)+3*mean(S)*sqrt(1-c4(n)^2)/c4(n)
plot_chart(M,LIC=LICm,LSC=LSCm,Type = "carte de la moyenne")
plot_chart(S,LIC=LICs,LSC=LSCs,Type = "carte de l'écart type")

3.2 Carte EWMA

3.2.1 Introduction

La carte de Shewhart de la moyenne est très simple à mettre en oeuvre et à interpréter. Cependant elle n’a pas une très grande efficacité surtout :

  • en cas de faibles et moyennes déviations

  • en cas de structure d’autocorrélation, c’est à dire lorsque le passé a une influence, par exemple lorsqu’une tendance croissante apparaît.

Exemple :

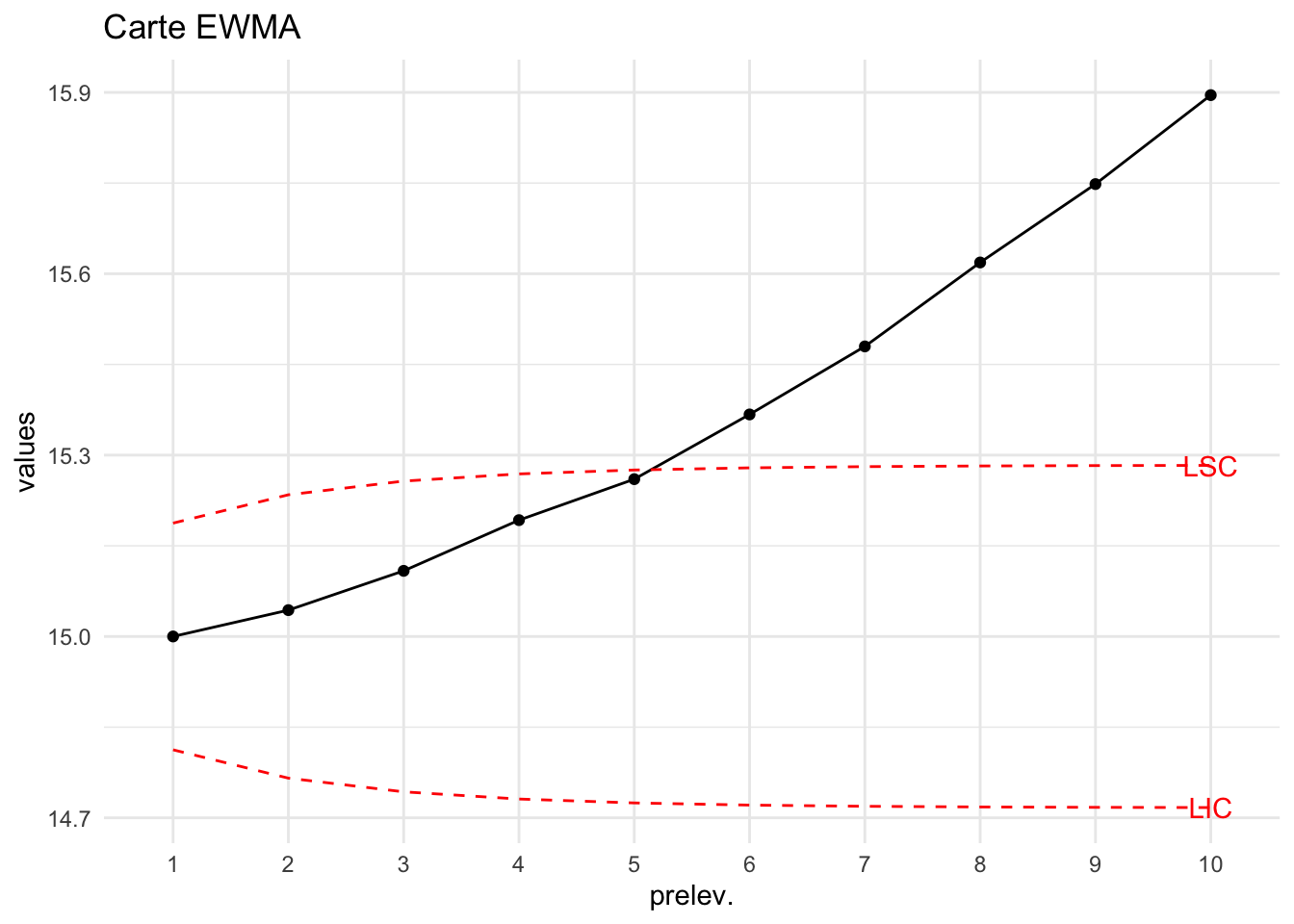
On suit une production de caractéristique \(\mu=15\) et \(\sigma=0.5\). Pour ce faire 10 prélèvements de 4 unités de production ont été réalisés. On construit la carte de moyenne de Shewhart. A partir du 7ième prélèvement on constate une déviation de la moyenne et un décentrage supérieur. La carte de Shewhart ne détecte cette déviation que très tardivement (14ième prélèvement).

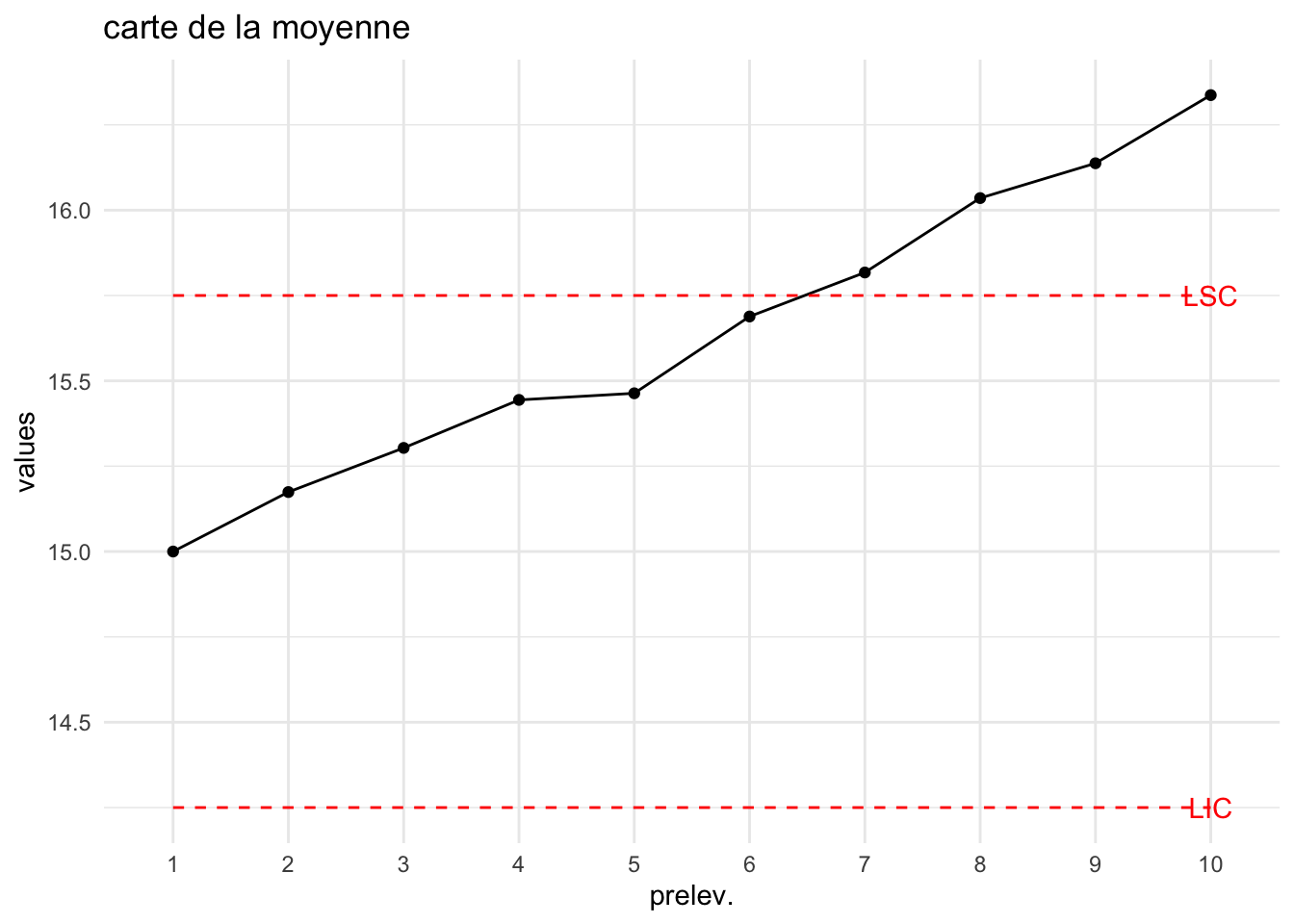
Une des solutions est la carte EWMA

3.2.2 Définition des cartes EWMA

EWMA : Exponentially Weighted Moving Average

On définit la statistique \(z_i\) par une relation de récurrence pour tout \(i=1,...,k\)

\[ z_i=\lambda \bar x_i +(1-\lambda)z_{i-1}, \]

où \(\bar x_i\) est la moyenne des unités pour le prélèvement \(i\) et \(0<\lambda\leq 1\) est un réel qui sera choisi en fonction du poids que l’on veut donner aux données précédentes. En effet, en général on choisit \(z_0=\mu\) (moyenne du procédé de fabrication). On a \[ \begin{cases} z_1=\lambda \bar x_1+(1-\lambda)\mu \\ z_2=\lambda \bar x_2+(1-\lambda)z_1= \lambda \bar x_2+\lambda(1-\lambda)\bar x_1+(1-\lambda)^2\mu \\ z_3=\lambda \bar x_3+\lambda(1-\lambda)\bar x_2+\lambda(1-\lambda)^2\bar x_1+ (1-\lambda)^3\mu \\ \ldots \end{cases} \]

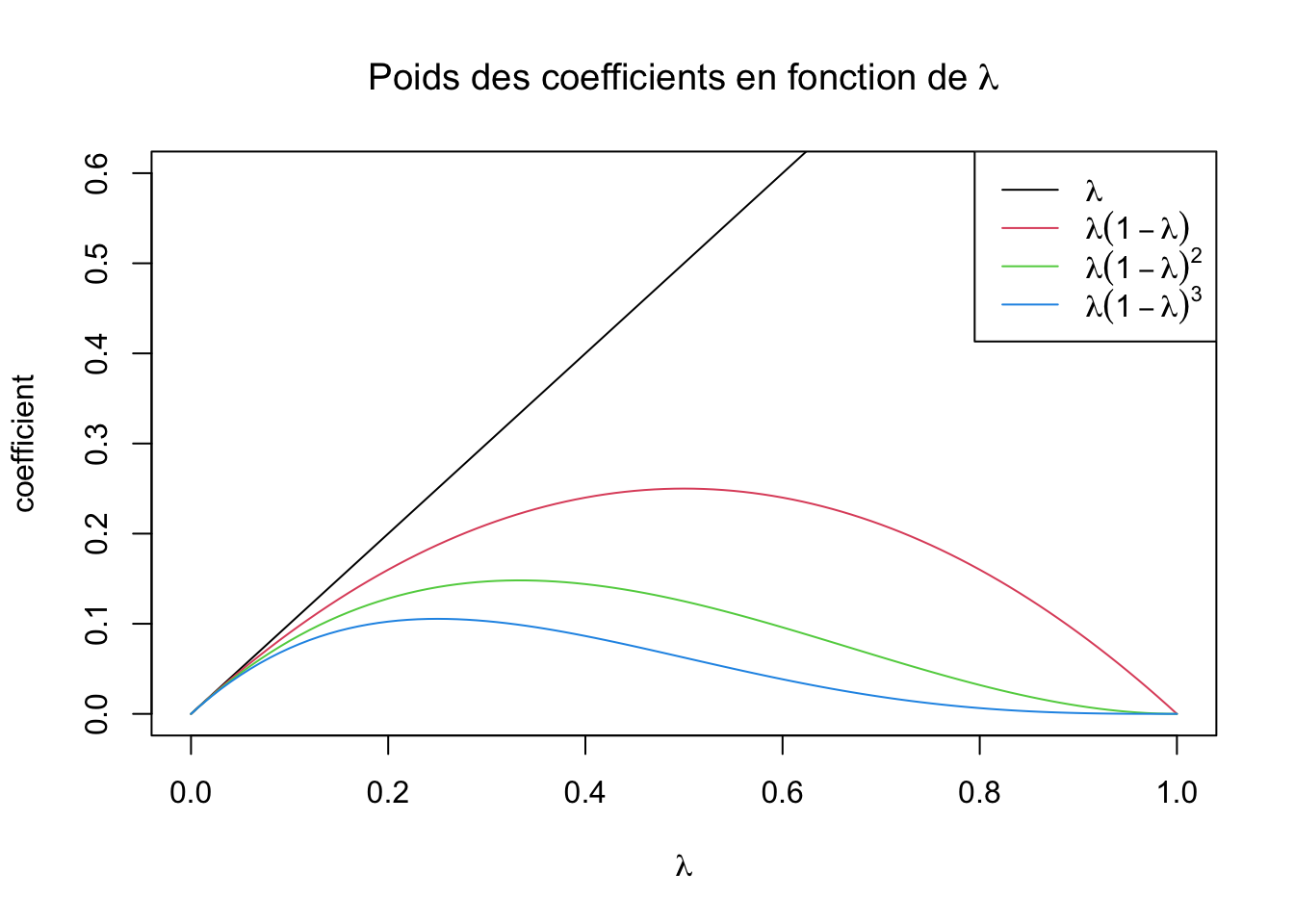
  • La cas \(\lambda=1\) correspond à la carte de Shewhart sur la moyenne.

  • On constate que \(\bar x_i\) a une importance d’autant plus importante dans \(z_i\) que \(\lambda\) est grand.

  • En général on utilise \(0.25<\lambda<0.5\).

3.2.3 Limites de contrôle des cartes EWMA

Les limites de ces cartes sont variables (en fonction de \(i\)) pour \(X\sim \mathcal N(\mu,\sigma)\) on a :\[LC = \mu \pm L\frac{\sigma}{\sqrt{n}}\times \sqrt {\frac{\lambda}{2-\lambda}[1-(1-\lambda)^{2i}] },\] en général avec \(L=3\).

Lorsque le nombre \(i\) de prélèvement est très grand alors \(LC = \mu \pm L\frac{\sigma}{\sqrt{n}}\times \sqrt {\frac{\lambda}{2-\lambda}}\). Dans ce cas on peut jouer sur ce paramètre \(L\) pour améliorer l’efficacité de la carte en fonction de \(\lambda\).

3.2.4 Retour à l’exemple :

On constate que contrairement à la carte de la moyenne la carte EWMA détecte le décentrage dès le 5ième prélèvement.

lambda=0.25
Z<-ewma_cart1(data,n,mu=mu,sig=sig,lambda=lambda)
plot_chart(Z$z,LIC=Z$LIC,LSC=Z$LSC,Type="Carte EWMA")