3  Partition consensuelle

3.1 Mesure d’accord entre deux partitions

On demande à 2 participants de partager en groupes 5 produits numérotés \(\{1,2,3,4,5\}\) On obtient les deux partitions suivantes : \(P_1=\{ \{1,2,3\},\{4,5\} \}\) et \(P_2=\{ \{1,2\},\{3,4,5\} \}\). On va mesurer l’accord entre ces deux partitions en regardant si chaque paire de produits est groupé dans \(P_1\) (Gr P1), séparé dans \(P_1\) (sep P1). De même dans \(P_2.\)

name

Produit 1

Produit 2

Produit 3

Produit 4

Produit 5

P1

1

1

1

2

2

P2

1

1

2

2

2

name

Gr P2

Sep P2

Gr P1

4

2

Sep P1

2

2

  • Courcoux et al. (2014) définissent le Rand Index \(RI(P_1,P_2)=\dfrac{a+d}{P(P-1)/2}\) où \(a+d\) est le nombre d’accord entre \(P_1,P_2\) (ie lorsqu’elles regroupent ou qu’elles séparent les deux produits).

  • On a \(0\leq RI(P_1,P_2) \leq 1\) (0 désaccord total et 1 accord total).

La fonction RandIndex du package FreeSortR permet d’effectuer ce calcul :

Voir le code R 
RandIndex(P1,P2)$Rand
[1] 0.6

3.2 Inconvénient

Il augmente en moyenne lorsque le nombre \(N\) de sujets augmente. La solution est de remplacer \(RI\) par \[ ARI(P_1,P_2)=\dfrac{RI(P_1,P_2)-\overline{RI}}{1-\overline{RI}} \]

où \(\overline{RI}\) est la moyenne du \(RI\) pour 2 partitions dont le consensus n’est dû qu’au hasard.

Conséquences

  1. \(ARI(P_1,P_2)=0\) lorsque le consensus n’est dû qu’au hasard,
  2. \(ARI(P_1,P_2)=1\) lorsque le consensus est parfait (ie les partitions sont identiques).
Voir le code R 
RandIndex(P1,P2)$AdjustedRand
[1] 0.1666667

3.3 Mesure de consensus basé sur \(ARI\)

  • On cherche une partition \(P\) telle que la moyenne des \(ARI\) de chaque sujet avec cette partition est maximale c’est à dire \(C_M(P)=\frac 1{N}\sum_{n=1}^N ARI(P,P_n)\) maximale.

  • On procède de façon itérative en fixant le nombre \(K\) de classes dans la partition consensuelle. On choisit la valeur de \(K\) pour laquelle \(C_M(P)\) est maximal.

  • Cet algorithme est sensible au choix de la première partition. Plusieurs choix sont proposés dans FreeSorteR on choisira :

Voir le code R 
cons=ConsensusPartition(tl,ngroups=0,type="fusion")

Fusion algorithm. May be time consuming.

3.4 Résultat pour l’exemple

Partition en 7 classes avec \(C_M(P)=0.308\)

name

.

Lemon

1

Grapefruit

1

Pineapple

1

Pear

1

Honey

2

Butter

3

Grilledbread

2

Grilledhazelnut

2

Strawberry

1

Raspberry

1

Cherry

4

Blackcurrant

3

Greenpepper

5

Smoked

6

Pepper

7

Licorice

6

3.5 Représentation de la partition consensuelle sur le plan latent :

Voir le code R 
config=getConfig(resMds)
colnames(config)=paste("Dim",1:3,sep="")
Consensus=as.factor(cons$Consensus)
ggplot(config,aes(x=Dim1,y=Dim2,label=rownames(config),color=Consensus))+
  geom_text()+
  xlab(paste("Dim1=",round(resMds@Percent[1]*100,1),"%"))+
  ylab(paste("Dim2=",round(resMds@Percent[2]*100,1),"%"))+
  ggtitle(paste("MDS, stress=",round(resMds@Stress,3)))+
  theme_minimal()+theme(legend.position = "none")

3.6 Classification des sujets

L’\(ARI\) permet de définir une distance entre les sujets, \[ d_{ARI}(S_i,S_j)=\sqrt{1-ARI(P_i,P_j)} \] où le sujet \(S_i\) propose la partition \(P_i.\)

3.6.1 CAH avec d_ARI

On peut alors réaliser une classification ascendante hierarchique avec cette distance :

Voir le code R 
i=j=1
d_ARI<-function(df,i,j){
  return(sqrt(1-RandIndex(df[,i],df[,j])$AdjustedRand))
}
N<-dim(df)[2]
M<-matrix(NA,nrow=N,ncol=N)
for(i in 1:N){
  for(j in 1:N){
    M[i,j]<-d_ARI(df,i,j)
  }
}

dd <- as.dist(M)

res<-hclust(dd,method="ward.D2")
plot(res,hang=-1,ylim=c(0,1.5))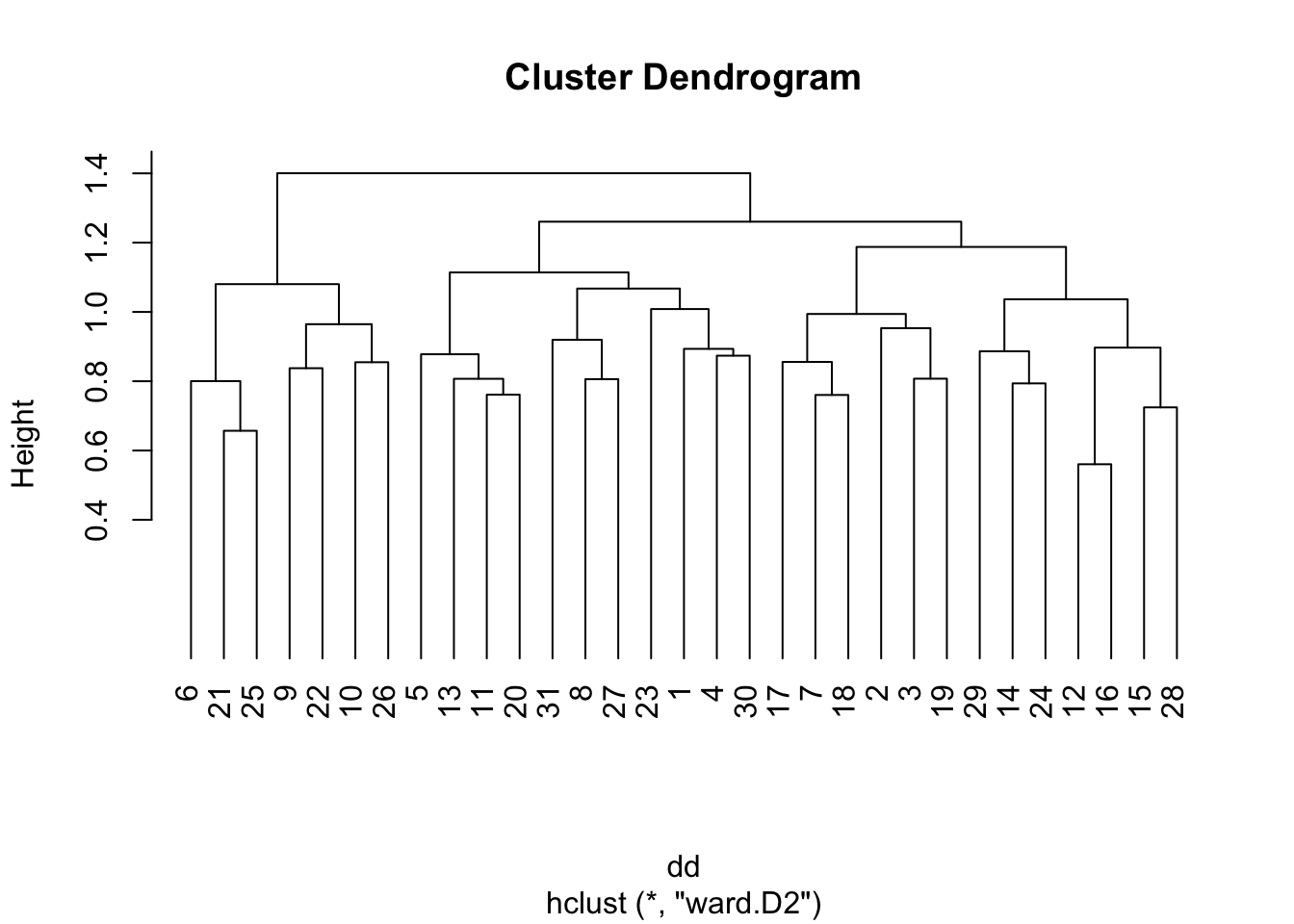

On choisit de former deux groupes d’individus :

Voir le code R 
gr<-cutree(res,2)

Ces groupes sont déséquilibrés et constitués de

Voir le code R 
flextable(as.data.frame(table(gr)))

gr

Freq

1

24

2

7

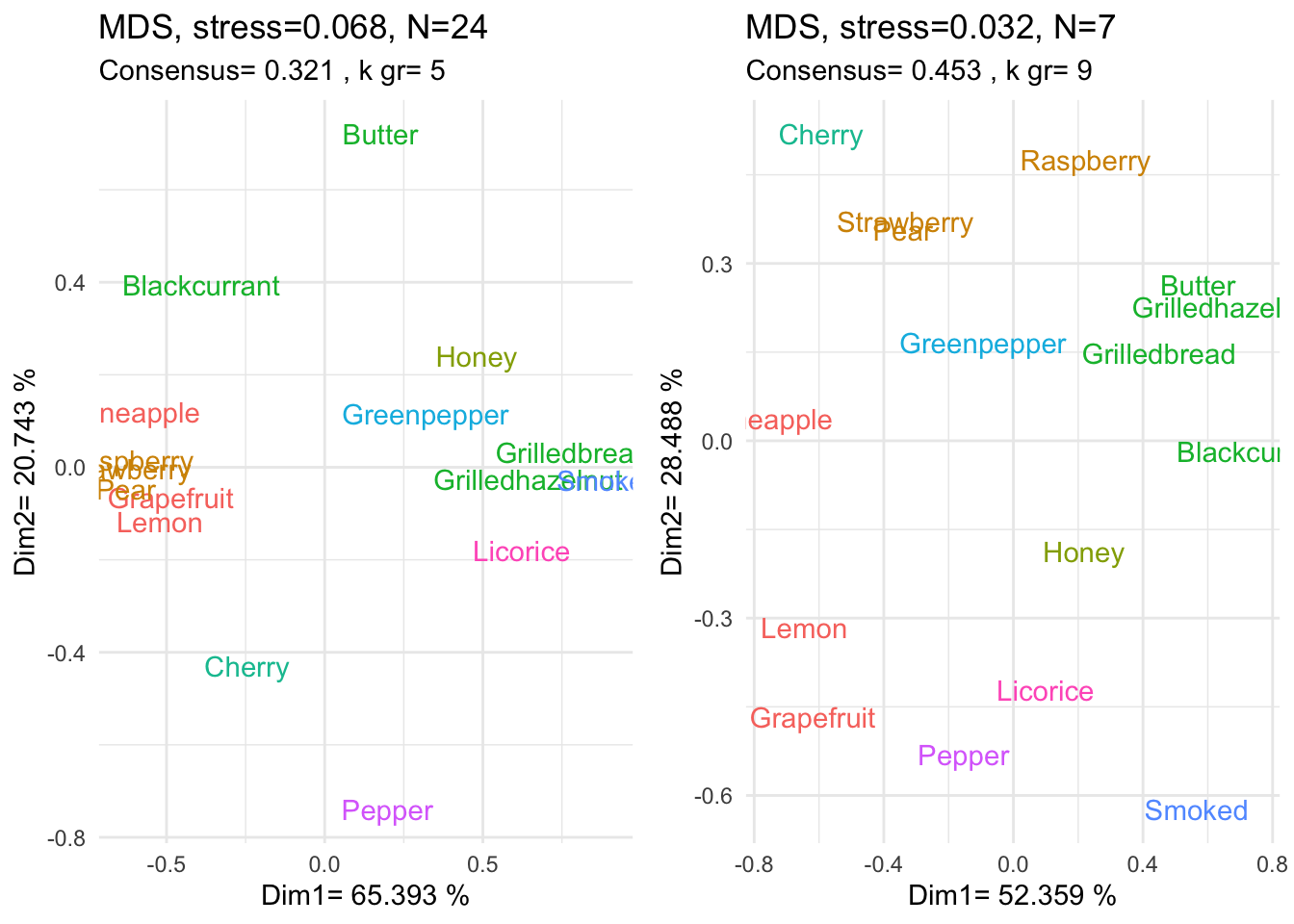
On peut ainsi mettre en évidence le consensus pour chacun de ces deux groupes :

Voir le code R 
df1<-df[,gr==1]
ndim=3
tl1<-SortingPartition(df1)
resMds1<-MdsSort(tl1,ndim=ndim)
config1<-getConfig(resMds1)
cons1<-ConsensusPartition(tl1,ngroups=0)
config1=getConfig(resMds1)
colnames(config1)=paste("Dim",1:ndim,sep="")
Consensus1=as.factor(cons1$Consensus)
p1=ggplot(config1,aes(x=Dim1,y=Dim2,label=rownames(config1),color=Consensus1))+
  geom_text()+
  xlab(paste("Dim1=",round(resMds1@Percent[1]*100,3),"%"))+
  ylab(paste("Dim2=",round(resMds1@Percent[2]*100,3),"%"))+
  labs(
    title=paste("MDS, stress=",round(resMds1@Stress,3),", N=",sum(gr==1),sep=""),
    subtitle = paste("Consensus=",round(cons1$Crit,3),", k gr=",max(cons1$Consensus)),sep="")+
  theme_minimal()+theme(legend.position = "none")

df1<-df[,gr==2]
tl1<-SortingPartition(df1)
resMds1<-MdsSort(tl1,ndim=ndim)
config1<-getConfig(resMds1)
cons1<-ConsensusPartition(tl1,ngroups=0)
config1=getConfig(resMds1)
colnames(config1)=paste("Dim",1:ndim,sep="")
Consensus1=as.factor(cons1$Consensus)
p2=ggplot(config1,aes(x=Dim1,y=Dim2,label=rownames(config1),color=Consensus1))+
  geom_text()+
  xlab(paste("Dim1=",round(resMds1@Percent[1]*100,3),"%"))+
  ylab(paste("Dim2=",round(resMds1@Percent[2]*100,3),"%"))+
  labs(
    title=paste("MDS, stress=",round(resMds1@Stress,3),", N=",sum(gr==2),sep=""),
    subtitle = paste("Consensus=",round(cons1$Crit,3),", k gr=",max(cons1$Consensus)),sep="")+
  theme_minimal()+theme(legend.position = "none")
grid.arrange(p1,p2,ncol=2)