Voir le code R
data("AromaSort")
df=AromaSort
nom_aromes <- read_excel("nom_aromes.xlsx",
col_names = FALSE)New names:
• `` -> `...1`
• `` -> `...2`Voir le code R
colnames(nom_aromes)<-c("EN","FR")
rownames(df)<-nom_aromes$FR2 Tri libre
Télécharger le fichier script_TL il servira pour la plupart des manipulations sur R.
On va étudier un premier exemple de tri libre de 16 arômes proposés à 31 sujets.
Cette base de données est disponible dans le package FreeSorteR. Dans la suite cette base de données sera désignée par df (dataframe). Les noms des aromes en FR sont disponibles dans ce fichier nom_aromes
On nommera les bases de données df pour plus de facilité pour la suite :
column name | S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | S12 | S13 | S14 | S15 | S16 | S17 | S18 | S19 | S20 | S21 | S22 | S23 | S24 | S25 | S26 | S27 | S28 | S29 | S30 | S31 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Citron | 5 | 1 | 4 | 1 | 1 | 1 | 1 | 2 | 3 | 1 | 1 | 1 | 1 | 4 | 2 | 1 | 2 | 2 | 2 | 3 | 3 | 4 | 3 | 1 | 2 | 6 | 1 | 2 | 8 | 1 | 1 |
pamplemousse | 5 | 3 | 5 | 1 | 2 | 1 | 2 | 2 | 3 | 1 | 1 | 1 | 1 | 4 | 2 | 1 | 1 | 2 | 1 | 2 | 3 | 6 | 3 | 1 | 2 | 6 | 1 | 2 | 2 | 1 | 1 |
ananas | 4 | 1 | 5 | 1 | 5 | 1 | 2 | 1 | 1 | 1 | 5 | 1 | 1 | 1 | 1 | 1 | 1 | 3 | 1 | 2 | 2 | 4 | 1 | 3 | 7 | 6 | 3 | 3 | 4 | 1 | 2 |
poire | 5 | 1 | 5 | 1 | 1 | 3 | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 1 | 3 | 5 | 4 | 2 | 3 | 6 | 1 | 1 | 3 | 4 | 1 | 1 |
miel | 4 | 2 | 3 | 2 | 3 | 6 | 3 | 5 | 2 | 3 | 7 | 2 | 1 | 4 | 5 | 5 | 3 | 1 | 5 | 4 | 4 | 3 | 1 | 2 | 2 | 7 | 5 | 4 | 12 | 1 | 1 |
beurre | 1 | 4 | 5 | 2 | 3 | 5 | 3 | 5 | 4 | 4 | 4 | 5 | 2 | 4 | 9 | 5 | 6 | 4 | 3 | 5 | 4 | 2 | 1 | 6 | 4 | 5 | 3 | 5 | 9 | 5 | 3 |
pain grillé | 1 | 2 | 3 | 5 | 5 | 5 | 3 | 3 | 2 | 3 | 9 | 2 | 3 | 2 | 3 | 2 | 3 | 1 | 4 | 1 | 4 | 2 | 4 | 6 | 4 | 4 | 2 | 1 | 1 | 5 | 3 |
noisettes grillées | 5 | 2 | 3 | 2 | 5 | 5 | 3 | 3 | 4 | 3 | 6 | 2 | 3 | 2 | 3 | 2 | 3 | 5 | 5 | 1 | 4 | 2 | 3 | 4 | 4 | 5 | 2 | 7 | 6 | 5 | 6 |
fraise | 5 | 1 | 5 | 1 | 1 | 2 | 2 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | 6 | 1 | 2 | 3 | 1 | 3 | 6 | 6 | 1 | 3 | 1 | 1 | 3 | 3 | 3 | 1 | 4 |
framboise | 3 | 3 | 4 | 4 | 1 | 2 | 2 | 1 | 4 | 4 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 5 | 2 | 2 | 3 | 1 | 1 | 3 | 3 | 4 | 4 | 4 |
cerise | 3 | 3 | 5 | 3 | 5 | 6 | 1 | 1 | 1 | 2 | 2 | 1 | 3 | 3 | 7 | 8 | 2 | 4 | 6 | 7 | 7 | 4 | 3 | 2 | 8 | 2 | 3 | 3 | 7 | 1 | 3 |
cassis | 3 | 4 | 4 | 3 | 4 | 5 | 2 | 5 | 4 | 3 | 7 | 1 | 2 | 4 | 1 | 1 | 4 | 3 | 6 | 5 | 4 | 1 | 2 | 1 | 4 | 7 | 1 | 3 | 9 | 3 | 2 |
poivre vert | 4 | 3 | 1 | 4 | 4 | 3 | 3 | 4 | 2 | 5 | 8 | 2 | 1 | 3 | 4 | 7 | 3 | 1 | 3 | 2 | 2 | 2 | 5 | 4 | 7 | 4 | 1 | 6 | 11 | 3 | 2 |
fumé | 2 | 2 | 2 | 4 | 3 | 4 | 3 | 4 | 7 | 3 | 3 | 3 | 5 | 2 | 4 | 3 | 5 | 1 | 5 | 9 | 1 | 5 | 6 | 2 | 3 | 3 | 2 | 1 | 10 | 5 | 5 |
poivre | 2 | 2 | 2 | 1 | 2 | 3 | 1 | 2 | 6 | 5 | 5 | 4 | 4 | 3 | 8 | 6 | 4 | 4 | 6 | 8 | 3 | 3 | 3 | 5 | 2 | 8 | 4 | 4 | 11 | 2 | 1 |
réglisse | 2 | 4 | 3 | 4 | 2 | 4 | 3 | 3 | 5 | 4 | 7 | 3 | 5 | 3 | 5 | 4 | 3 | 1 | 4 | 6 | 3 | 5 | 2 | 2 | 5 | 9 | 4 | 4 | 5 | 2 | 3 |
Voir le code R
tl<-SortingPartition(df)
DescriptionPartition(tl,subject=1)[1] "{Citron, pamplemousse, poire, noisettes grillées, fraise}{ananas, miel, poivre vert}{beurre, pain grillé}{framboise, cerise, cassis}{fumé, poivre, réglisse}"2.1 Matrice de dissimilarités individuelle
On note \(D^{(n)}=(d^{(n)}_{i,j})_{i,j}\) la matrice de dissimilarités obtenue à partir de la partition du \(n\)-ième individu. On a
\(d^{(n)}_{i,j}=0\) si \(i,j\) sont dans la même partition,
\(d^{(n)}_{i,j}=1\) sinon.
Remarque La matrice \(D^{(n)}\) est une matrice symétrique dont la diagonale est nulle.
2.1.1 Exemple individu 1 :
Voir le code R
ListDiss<-Dissimil(tl)
T1=as.data.frame(ListDiss[[1]])
rownames(T1)=tl@LabStim
colnames(T1)=tl@LabStimCeci donne la matrice de dissimilarité pour l’individu
name | Citron | pamplemousse | ananas | poire | miel | beurre | pain grillé | noisettes grillées | fraise | framboise | cerise | cassis | poivre vert | fumé | poivre | réglisse |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Citron | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
pamplemousse | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
ananas | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
poire | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
miel | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
beurre | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
pain grillé | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
noisettes grillées | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
fraise | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
framboise | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
cerise | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
cassis | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
poivre vert | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
fumé | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
poivre | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
réglisse | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
2.2 Matrice de dissimilarités à l’échelle du panel
On ajoute toutes les matrices de dissimilarités individuelles. On obtient la matrice \(D\) de coefficients : \[\delta_{i,j}=\sum_{n=1}^N d^{(n)}_{i,j}\]
Cette matrice est symétrique et sa diagonale est nulle.
Tous les coefficients de cette matrice sont des entiers inférieurs ou égaux à \(N\).
2.2.1 Retour sur l’exemple
Voir le code R
D<-DissTot(tl)
rownames(D)=tl@LabStimOn obtient la matrice de dissimilarité totale :
name | Citron | pamplemousse | ananas | poire | miel | beurre | pain grillé | noisettes grillées | fraise | framboise | cerise | cassis | poivre vert | fumé | poivre | réglisse |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Citron | 0 | 9 | 21 | 15 | 26 | 30 | 31 | 29 | 20 | 21 | 25 | 25 | 29 | 31 | 24 | 30 |
pamplemousse | 9 | 0 | 18 | 17 | 26 | 29 | 31 | 29 | 20 | 24 | 26 | 25 | 27 | 31 | 24 | 29 |
ananas | 21 | 18 | 0 | 15 | 27 | 28 | 30 | 30 | 14 | 20 | 22 | 24 | 25 | 31 | 29 | 31 |
poire | 15 | 17 | 15 | 0 | 28 | 30 | 31 | 30 | 11 | 14 | 23 | 24 | 28 | 31 | 27 | 30 |
miel | 26 | 26 | 27 | 28 | 0 | 23 | 22 | 22 | 28 | 30 | 28 | 25 | 24 | 24 | 26 | 23 |
beurre | 30 | 29 | 28 | 30 | 23 | 0 | 22 | 22 | 28 | 27 | 27 | 21 | 28 | 28 | 30 | 27 |
pain grillé | 31 | 31 | 30 | 31 | 22 | 22 | 0 | 12 | 31 | 30 | 28 | 27 | 24 | 23 | 30 | 24 |
noisettes grillées | 29 | 29 | 30 | 30 | 22 | 22 | 12 | 0 | 30 | 29 | 28 | 26 | 26 | 24 | 29 | 27 |
fraise | 20 | 20 | 14 | 11 | 28 | 28 | 31 | 30 | 0 | 14 | 22 | 26 | 30 | 31 | 30 | 31 |
framboise | 21 | 24 | 20 | 14 | 30 | 27 | 30 | 29 | 14 | 0 | 24 | 22 | 27 | 30 | 31 | 28 |
cerise | 25 | 26 | 22 | 23 | 28 | 27 | 28 | 28 | 22 | 24 | 0 | 26 | 29 | 30 | 26 | 28 |
cassis | 25 | 25 | 24 | 24 | 25 | 21 | 27 | 26 | 26 | 22 | 26 | 0 | 27 | 30 | 29 | 28 |
poivre vert | 29 | 27 | 25 | 28 | 24 | 28 | 24 | 26 | 30 | 27 | 29 | 27 | 0 | 26 | 27 | 26 |
fumé | 31 | 31 | 31 | 31 | 24 | 28 | 23 | 24 | 31 | 30 | 30 | 30 | 26 | 0 | 28 | 22 |
poivre | 24 | 24 | 29 | 27 | 26 | 30 | 30 | 29 | 30 | 31 | 26 | 29 | 27 | 28 | 0 | 24 |
réglisse | 30 | 29 | 31 | 30 | 23 | 27 | 24 | 27 | 31 | 28 | 28 | 28 | 26 | 22 | 24 | 0 |
2.3 MDS (Multi Dimensionnal Scaling)
On considère \(N\) points \(x_1,...,x_N\) dans un espace de dimension \(P\) caractérisés par la matrice de dissimilarité \(D=(\delta_{ij})_{1\leq i\leq j\leq N}\).
BUT représenter ces points dans un espace de dimension \(k<P\) par \(N\) points \(y_1,...,y_N\) en conservant les proximités entre les points initiaux.
Cela suppose :
l’existence de variables latentes (ie qui permettent de résumer des dissimilarités entre produits)
le choix d’un indice de qualité de la projection des dissimilarités dans l’espace latent (\(\leadsto\) S : Fonction de coût appelée Stress). Le but sera de trouver \(y_1,...,y_N\) tels que \(S(y_1,...,y_N)\) est minimale.
2.3.1 MDS Métrique
Dans ce cas le stress est défini par \[ S(y_1,...,y_N)=\sum_{i< j} \left( \delta_{ij}-\Vert y_i-y_j\Vert\right)^2 \] Dans ce cas on veut représenter les points initiaux en conservant la valeur absolue et relative de leurs dissimilarités.
2.3.2 MDS non Métrique
Dans ce cas le stress est défini par \[ S(y_1,...,y_N)=\sum_{i< j} \left( \delta_{ij}-f(\Vert y_i-y_j\Vert)\right)^2 \] où \(f\) est une fonction monotone de \((i,j)\). La fonction \(f\) s’adapte durant la phase d’optimisation.
On veut préserver uniquement l’ordre entre les proximités des points initiaux.
2.4 Le stress normalisé
La fonction de coût utilisé en pratique est une version normalisée du stress :
\[ S_{norm}(y_1,...,y_N)=\displaystyle \frac{\sum_{i<j}(\delta_{i,j}-f(\Vert y_i-y_j\Vert))^2}{\sum_{i<j}\delta_{i,j}^2} \]
où \(f\) est l’identité pour la MDS métrique.
2.5 Choix du nombre de dimension du MDS
Comme souvent en analyse de données, on peut utiliser la règle du coude pour déterminer le nombre de dimensions :
Voir le code R
stress<-rep(NA,6)
# getStress donne le stress de Kruskal (ie normalisé)
for(i in 1:6){
resMds<-MdsSort(tl,ndim=i,metric = T)
stress[i]<-getStress(resMds)
}
plot(1:6,stress,type="b",pch=20,
xlab="Nombre de dimensions",
col="purple")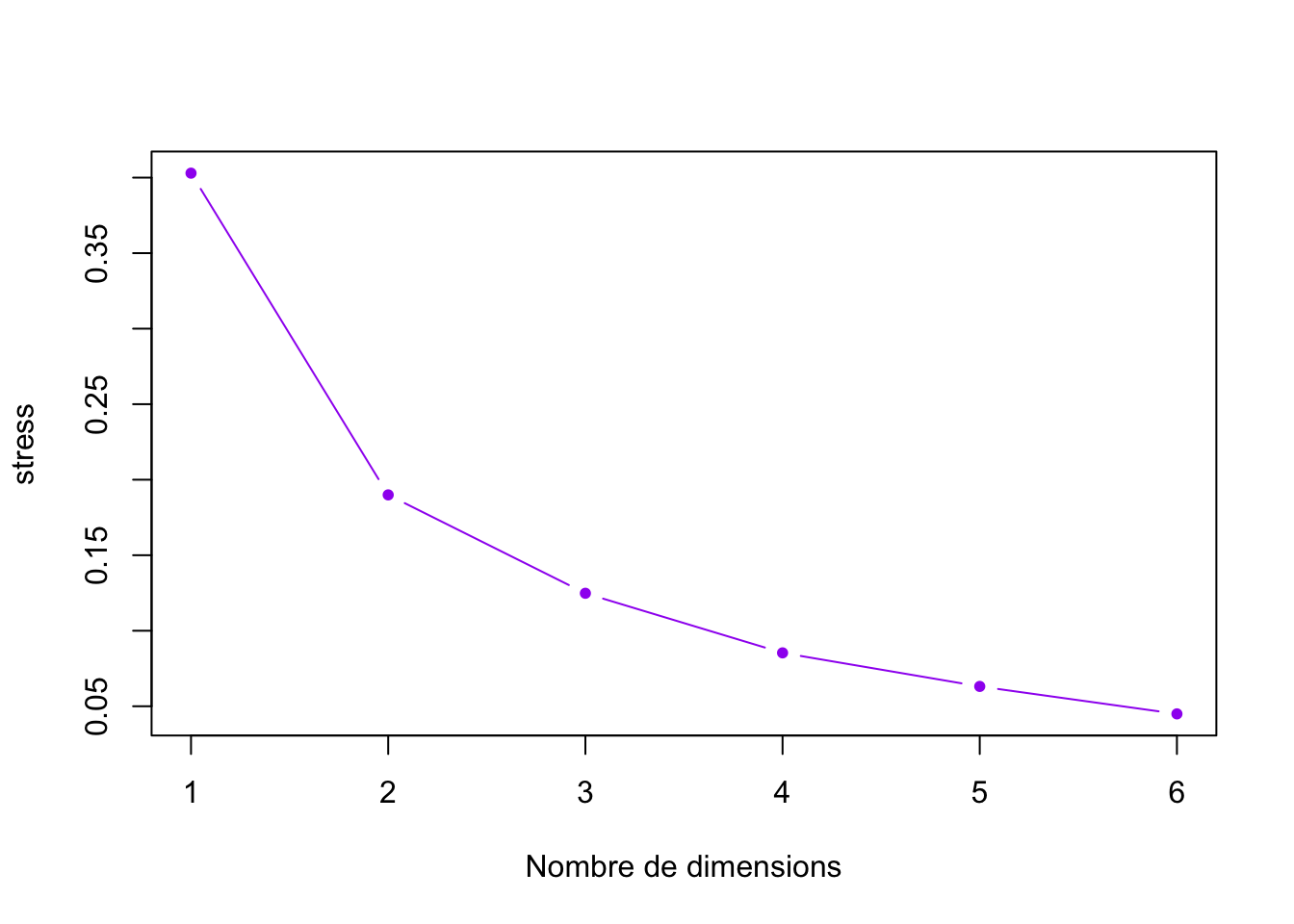
2.6 Représentation obtenue
Voir le code R
ndim=3
resMds<-MdsSort(tl,ndim=ndim,metric = T)
config<-getConfig(resMds)
config=as.data.frame(config)
colnames(config)=paste("Dim",1:ndim,sep="")
p1<-ggplot(config,aes(x=Dim1,y=Dim2,label=rownames(config)))+geom_text()+
ggtitle(paste("MDS, Stress=",round(resMds@Stress,3)))+
xlab(paste("Dim1",round(100*resMds@Percent[1],1),"%",sep=" "))+
ylab(paste("Dim2",round(100*resMds@Percent[2],1),"%",sep=" "))+
theme_minimal()
p2<-ggplot(config,aes(x=Dim2,y=Dim3,label=rownames(config)))+geom_text()+
ggtitle(paste("MDS, Stress=",round(resMds@Stress,3)))+
xlab(paste("Dim2",round(100*resMds@Percent[2],1),"%",sep=" "))+
ylab(paste("Dim3",round(100*resMds@Percent[3],1),"%",sep=" "))+
theme_minimal()
library(gridExtra)
Attaching package: 'gridExtra'The following object is masked from 'package:dplyr':
combineVoir le code R
grid.arrange(p1,p2,ncol=2)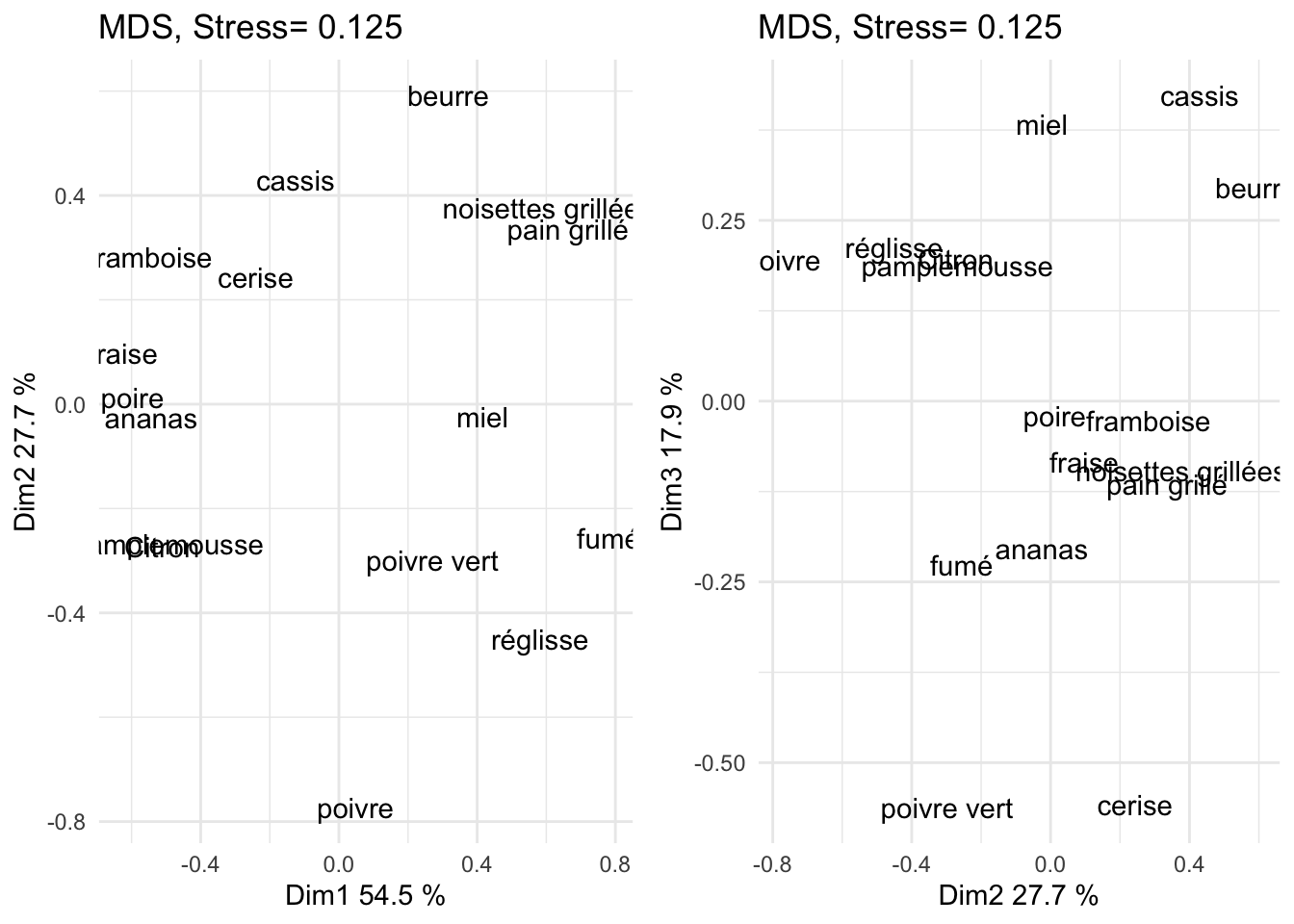
2.7 Ellipses de confiance
On se pose la question de la stabilité de la configuration. D’autres individus proposeraient d’autres partitions \(\leadsto\) autre configuration.
Pseudo-individus à partir des individus de l’échantillon (Bootstrap) : on tire des individus avec remise dans l’échantillon et on construit la configuration obtenue (en général \(B=500\) tirages).
Construction d’ellipses de confiance à partir de ces \(B\) configurations.
Voir le code R
resMds<-MdsSort(tl,ndim=ndim,metric = T,nboot=500)
p1=plot_MDS(resMds,1,2)
p2=plot_MDS(resMds,1,3)
grid.arrange(p1,p2,ncol=2)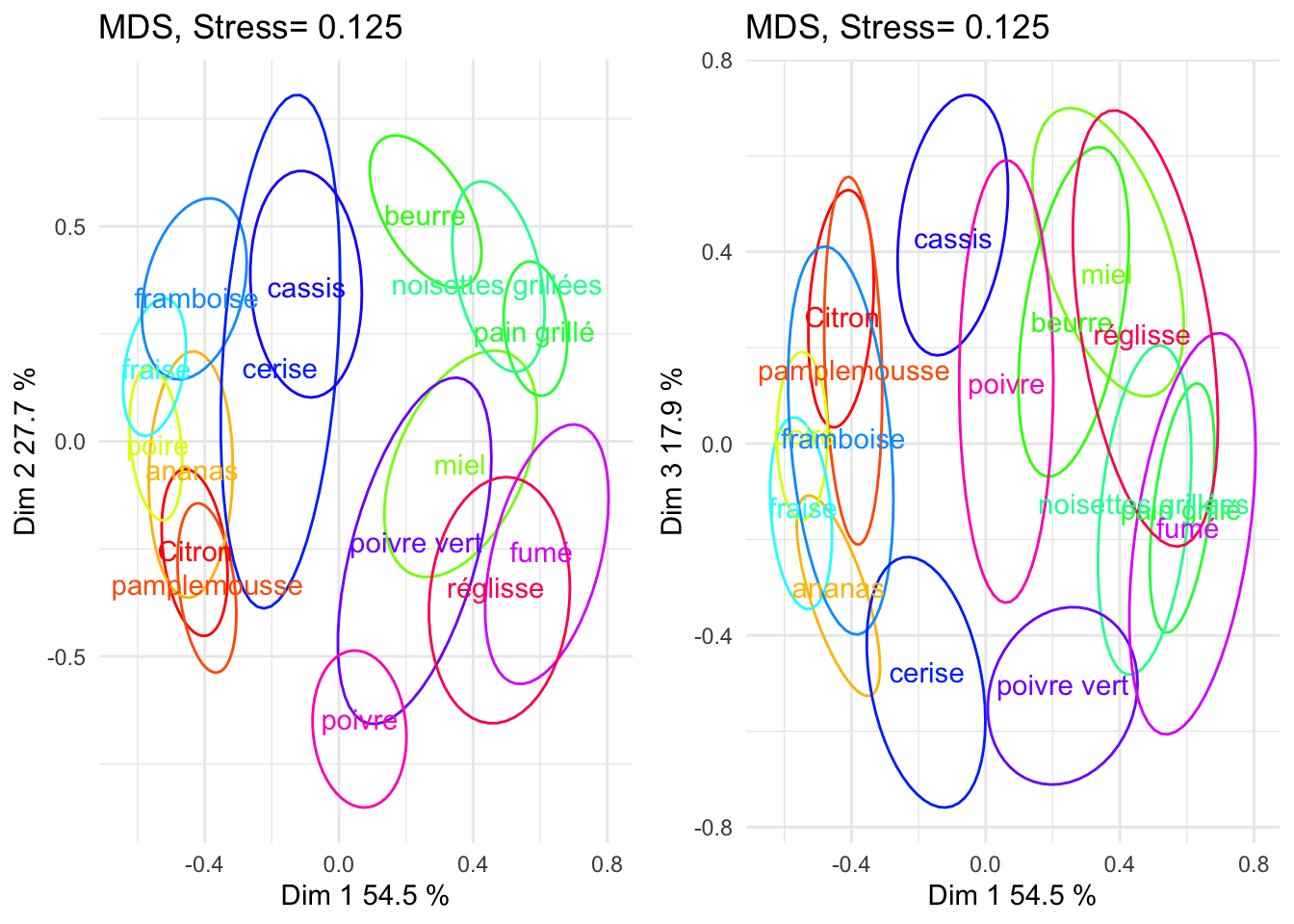
2.8 Informations additionnelles
On propose aux 31 sujets une liste de 36 descripteurs pour les 16 produits considérés. On obtient la table de contingence suivante :
name | Acid | Smoked | Heady | Citrus | Lemon | Cake | Milk | Woody | Grain | Low | Redfruit | Grilled | Strong | Fat | Vegetal | Medicine | Chemical | Licorice | Bread | Alcohol | Almond | Caramel | Coal | Unpleasant | Soft | Pepper | Flower | Fresh | Red | Fruit | Natural | Spicy | Sugar | Hot | Pleasant | Candy |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Lemon | 3 | 0 | 1 | 7 | 11 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 3 | 0 | 2 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 3 | 5 | 1 | 11 | 0 | 1 | 5 | 2 | 3 | 5 |
Grapefruit | 5 | 0 | 1 | 9 | 9 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 3 | 0 | 2 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 2 | 4 | 1 | 13 | 0 | 1 | 4 | 2 | 2 | 3 |
Pineapple | 5 | 0 | 1 | 5 | 4 | 0 | 0 | 4 | 0 | 0 | 3 | 0 | 3 | 0 | 4 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 3 | 0 | 1 | 3 | 3 | 13 | 0 | 1 | 9 | 0 | 2 | 8 |
Pear | 2 | 0 | 1 | 4 | 5 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 3 | 0 | 2 | 0 | 1 | 1 | 0 | 0 | 2 | 0 | 0 | 1 | 2 | 2 | 0 | 4 | 1 | 15 | 1 | 0 | 10 | 0 | 2 | 13 |
Honey | 1 | 2 | 1 | 1 | 3 | 0 | 1 | 3 | 2 | 0 | 0 | 2 | 7 | 0 | 2 | 1 | 0 | 0 | 0 | 2 | 1 | 1 | 1 | 8 | 2 | 1 | 2 | 3 | 0 | 1 | 1 | 1 | 4 | 3 | 1 | 1 |
Butter | 2 | 1 | 0 | 0 | 0 | 0 | 5 | 0 | 3 | 2 | 0 | 2 | 3 | 6 | 1 | 0 | 0 | 0 | 0 | 1 | 2 | 2 | 0 | 4 | 3 | 0 | 0 | 1 | 0 | 2 | 0 | 1 | 3 | 1 | 1 | 2 |
Grilledbread | 0 | 5 | 1 | 0 | 0 | 1 | 1 | 2 | 3 | 1 | 0 | 5 | 5 | 1 | 3 | 0 | 0 | 0 | 2 | 0 | 1 | 3 | 1 | 8 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 0 | 0 |
Grilledhazelnut | 0 | 3 | 1 | 1 | 0 | 2 | 1 | 3 | 6 | 1 | 0 | 3 | 4 | 1 | 2 | 0 | 1 | 0 | 1 | 0 | 1 | 2 | 0 | 5 | 2 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 2 | 3 | 1 | 0 |
Strawberry | 3 | 0 | 1 | 3 | 2 | 0 | 0 | 0 | 0 | 0 | 5 | 0 | 3 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | 1 | 3 | 0 | 0 | 4 | 5 | 14 | 0 | 0 | 13 | 0 | 2 | 14 |
Raspberry | 1 | 1 | 1 | 1 | 3 | 0 | 0 | 0 | 0 | 2 | 2 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 3 | 5 | 0 | 1 | 4 | 2 | 12 | 1 | 0 | 10 | 0 | 2 | 9 |
Cherry | 1 | 1 | 1 | 1 | 1 | 2 | 1 | 3 | 1 | 2 | 1 | 0 | 1 | 1 | 1 | 1 | 2 | 0 | 0 | 2 | 9 | 0 | 0 | 0 | 4 | 0 | 0 | 1 | 1 | 4 | 0 | 0 | 5 | 2 | 3 | 5 |
Blackcurrant | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 4 | 0 | 0 | 1 | 0 | 1 | 0 | 2 | 0 | 2 | 5 | 1 | 2 | 3 | 1 | 8 | 1 | 0 | 4 | 3 | 1 | 2 |
Greenpepper | 3 | 3 | 0 | 1 | 1 | 1 | 0 | 6 | 0 | 1 | 0 | 2 | 1 | 0 | 8 | 1 | 0 | 0 | 0 | 1 | 0 | 2 | 1 | 5 | 0 | 1 | 2 | 4 | 0 | 1 | 1 | 0 | 2 | 2 | 1 | 0 |
Smoked | 0 | 19 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 6 | 7 | 0 | 0 | 2 | 1 | 0 | 0 | 1 | 0 | 1 | 3 | 4 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 2 | 0 | 1 |
Pepper | 3 | 1 | 0 | 1 | 3 | 0 | 1 | 2 | 0 | 0 | 1 | 1 | 2 | 0 | 2 | 1 | 2 | 0 | 0 | 1 | 1 | 0 | 0 | 2 | 2 | 8 | 0 | 1 | 1 | 1 | 1 | 4 | 1 | 7 | 1 | 1 |
Licorice | 1 | 5 | 1 | 0 | 1 | 0 | 0 | 2 | 0 | 1 | 0 | 2 | 5 | 1 | 0 | 3 | 2 | 3 | 0 | 3 | 0 | 1 | 1 | 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 0 | 4 | 0 | 1 |
2.9 Caractérisation des axes latents
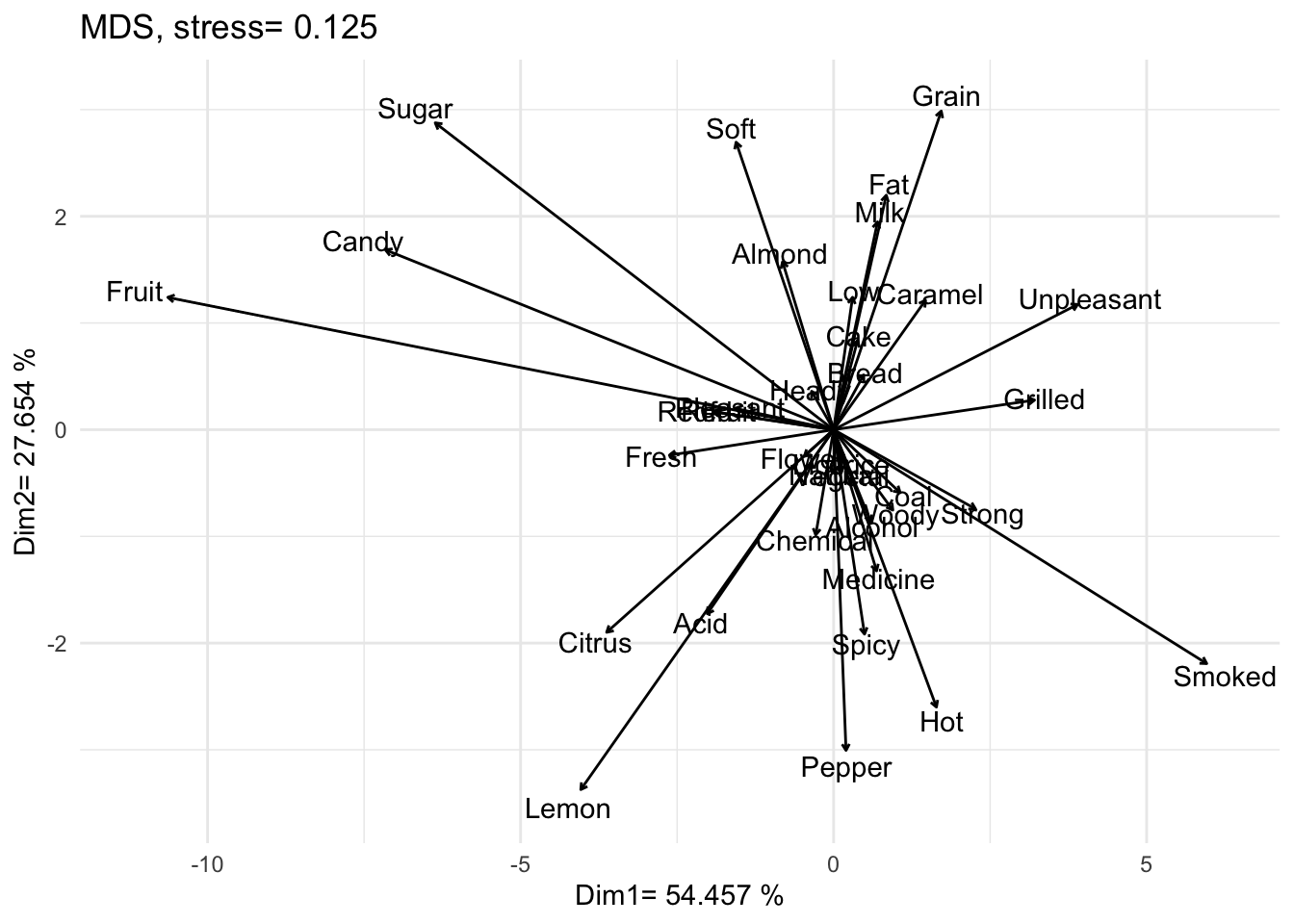
On effectue la régression de chacun des descripteurs sur les composantes de la MDS.
Les coefficients de regression seront utilisés comme coordonnées dans les plans factoriels.
Exemple
Descripteur Acide :
Voir le code R
beta<-data.frame(matrix(NA,nrow=dim(ia)[2],ncol=dim(config)[2]))
for(i in 1:dim(beta)[1]){
beta[i,]<-coef(lm(AromaTerms[,i]~as.matrix(config)))[-1]
}
rownames(beta)<-colnames(ia)
colnames(beta)[1:ndim]<-paste("Dim",1:ndim,sep="")On obtient :
name | Dim1 | Dim2 | Dim3 |
|---|---|---|---|
Acid | -2.01794673 | -1.7249668 | 0.1064646 |
Smoked | 5.95945509 | -2.1921155 | -3.5515100 |
Heady | -0.35189402 | 0.3600541 | 0.2250707 |
Citrus | -3.62536087 | -1.8989421 | 1.1125966 |
Lemon | -4.03865496 | -3.3728931 | 2.9779419 |
Cake | 0.38257879 | 0.8362063 | -1.1839306 |
Milk | 0.70194748 | 1.9483285 | 1.6124515 |
Woody | 0.94534488 | -0.7535015 | -2.7416106 |
Grain | 1.71912548 | 2.9864711 | 0.7676216 |
Low | 0.30250542 | 1.2412491 | -0.2532134 |
Redfruit | -1.93020060 | 0.1686525 | -0.4994624 |
Grilled | 3.20936191 | 0.2778622 | -0.7166606 |
Strong | 2.26661154 | -0.7428000 | 1.4970251 |
Fat | 0.84107596 | 2.1979908 | 1.2382889 |
Vegetal | 0.12128607 | -0.4052856 | -1.9195814 |
Medicine | 0.68638031 | -1.3234405 | -0.1490178 |
Chemical | -0.28615063 | -0.9865095 | -0.4348097 |
Licorice | 0.11880756 | -0.3071309 | 0.7666882 |
Bread | 0.48032605 | 0.5134819 | -0.2474069 |
Alcohol | 0.59188403 | -0.8627170 | 0.6019463 |
Almond | -0.81562514 | 1.5740392 | -3.2498261 |
Caramel | 1.46743166 | 1.2128476 | 0.1082160 |
Coal | 1.06241073 | -0.5905547 | -0.5755819 |
Unpleasant | 3.89826699 | 1.1746100 | 0.7644798 |
Soft | -1.55828617 | 2.6946415 | 0.7280814 |
Pepper | 0.19749672 | -3.0056491 | 1.2985158 |
Flower | -0.46849715 | -0.2494380 | 0.8513278 |
Fresh | -2.62314094 | -0.2391484 | 0.4562088 |
Red | -1.93020060 | 0.1686525 | -0.4994624 |
Fruit | -10.63468926 | 1.2409353 | 1.5327095 |
Natural | 0.01204305 | -0.4027629 | 0.4577618 |
Spicy | 0.49299547 | -1.9160446 | 1.3050949 |
Sugar | -6.36364574 | 2.8760189 | -1.1974220 |
Hot | 1.64211036 | -2.5999666 | 1.8823408 |
Pleasant | -1.57492256 | 0.2003923 | -0.5620110 |
Candy | -7.15916469 | 1.6855862 | -1.9332767 |
2.10 Représentation graphique
Voir le code R
ggplot(beta, aes(x=1.05*Dim1, y=1.05*Dim2,label=rownames(beta))) +
geom_text() +
geom_segment(data=beta,aes(x=0, y=0, xend=Dim1, yend=Dim2), arrow = arrow(length=unit(.1, 'cm')))+
theme_minimal()+
#theme(element_text(size=10))+
xlab(paste("Dim1=",round(resMds@Percent[1]*100,3),"%"))+
ylab(paste("Dim2=",round(resMds@Percent[2]*100,3),"%"))+
ggtitle(paste("MDS, stress=",round(resMds@Stress,3)))