library(lavaan)
library(semTools)
library(dplyr)
library(tidySEM)
library(readxl)
library(kableExtra)
library(DT)Vous pouvez installer les packages lavaan et semTools
Yves Rosseel (2012). lavaan: An R Package for Structural Equation Modeling. Journal of Statistical Software, 48(2), 1-36. https://doi.org/10.18637/jss.v048.i02
Jorgensen, T. D., Pornprasertmanit, S., Schoemann, A. M., & Rosseel, Y. (2022). semTools: Useful tools for structural equation modeling. R package version 0.5-6. Retrieved from https://CRAN.R-project.org/package=semTools
Jeu de données
Sentiment de sécurité mesurée par 5 items (ex : Certains enfants ont peur de se faire voler des affaires à l’école/au collège)
Rapport aux évaluations mesurée par 5 items,
Satisfaction classe mesurée par 5 items,
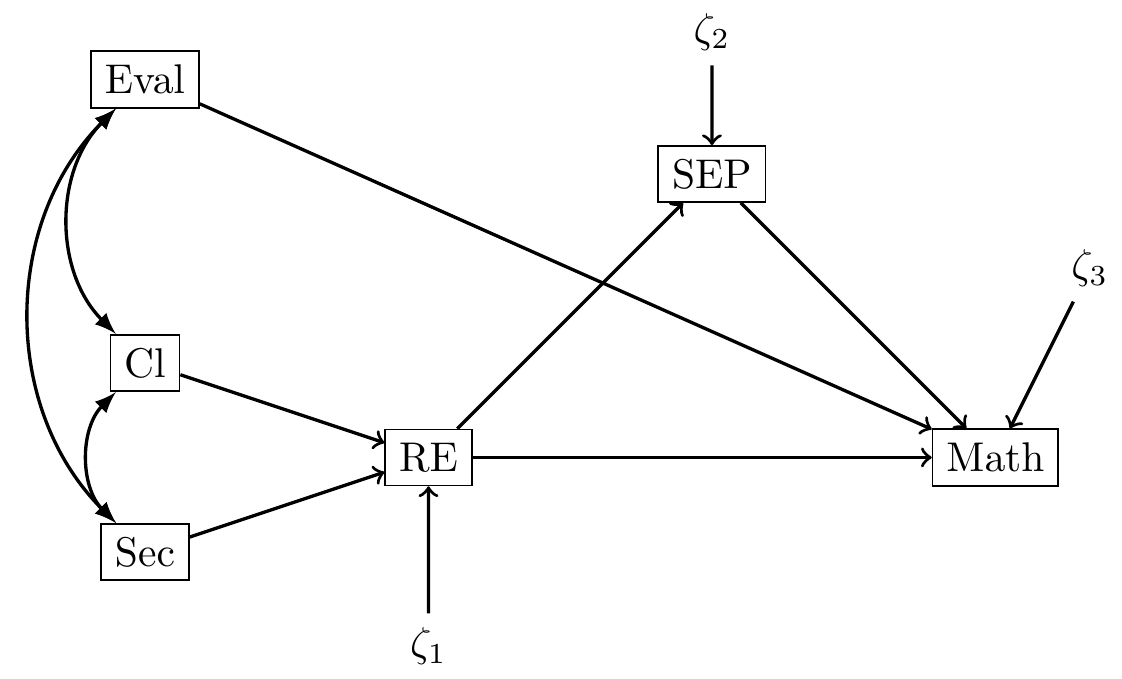
Modèle sur variables observées
Les données sont ici
On a calculé les moyennes des items pour chaque variable impliquée dans le modèle ci-dessous.
On peut commencer par regarder la matrice de corrélations des variables impliquées dans le modèle :
df=read.csv("data_agreg.csv")
df<-na.omit(df[,-1])
library(psych)
datatable(df)corrplot::corrplot(cor(df[,c("Math","SEP","RE","Sec","Eval","Cl")]),type="upper", method="number")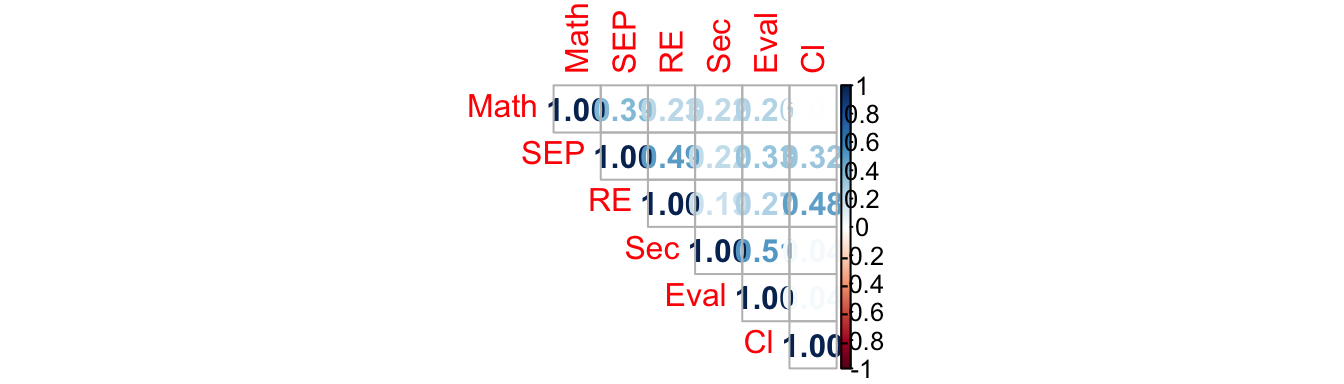
Dans lavaan, le modèle est tout d’abord spécifié :
Les régressions sont définis comme dans lm via ~ :
model1<-'
SEP~ RE
Math~ RE + SEP+Eval
RE~Sec+Cl
Eval~~Sec
Eval~~Cl
Cl~~Sec
'Ensuite on ajuste le modèle sur les données : l’argument fixed.x=F est obligatoire car dans un modèle de type Path analysis les variables exogènes sont supposées déterministes et ici ce n’est pas la cas dans la mesure où on estime une covariance entre elles.
fit<-sem(model1,data=df,fixed.x=FALSE)On peut accéder aux indices de fit et aux estimations et test des paramètres. Les tests sur les paramètres sont des tests de Wald, les intervalles de confiances sont construits par delta-méthode.
ind<-fitmeasures(fit) %>% as.data.frame()
colnames(ind)<-"Valeur"
ind %>% datatable() %>%
formatRound(columns = "Valeur",digits=3)parameterestimates(fit,standardized = T) %>% datatable() %>%
formatRound(columns = 4:12,digits=3)On peut être également intéressé par l’estimation de l’effet indirect dans le cadre de la médiation, c’est à dire l’effet produit \(a*b\) si on revient aux notations précédentes. On peut obtenir via lavaan une estimation de cet effet
model2<-'
SEP~ a*RE
Math~ c*RE + b*SEP+Eval
RE~Sec+Cl
Eval~~Sec
Eval~~Cl
Cl~~Sec
I:=a*b
T:=a*b+c
'fit1<-sem(model2,data=df,fixed.x=FALSE)
fit1 %>% parameterestimates(standardized = T) %>% filter(label %in% c("a","b","I")) %>% datatable() %>%
formatRound(columns = 4:12,digits=3)L’intervalle de confiance de l’effet indirect est dans les analyses de médiation par BCa-bootstrap :
fit2=sem(model2, data =df,se = "bootstrap", bootstrap = 500)
fit2 %>% parameterestimates(standardized = T,boot.ci.type="bca") %>% filter(label %in% c("a","b","I")) %>% datatable() %>%
formatRound(columns = 4:12,digits=3)Modèle à variables latentes
Les données sont ici. Dans cette situation il s’agit des données brutes, les réponses données sur les questionnaires sont cotées de 1 à \(k\).
df=read.csv("data.csv")
df %>% datatable() Les variable latentes sont exprimées via =~ dans le modèle lavaan.
model<-'
## Modèle de mesure
SEP=~SEP1+SEP2+SEP3+SEP4+SEP5
RE=~RE1+RE2+RE3+RE4+RE5
Eval=~Eval1+Eval2+Eval3+Eval4+Eval5
Cl=~Cl1+Cl2+Cl3+Cl4
Sec=~Sec1+Sec2+Sec3+Sec4+Sec5
## Régressions
SEP~ a*RE
Math~ c*RE + b*SEP+Eval
RE~Sec+Cl
Eval~~Sec
Eval~~Cl
Cl~~Sec
## Effets
I:=a*b
T:=a*b+c
'
fit<-sem(model,data=df,fixed.x=FALSE,estimator="MLR")
fit %>% fitmeasures() %>%as.data.frame() %>% datatable() %>% formatRound(colum=1,digits=3)Les indices CFI et TLI ne sont pas interprétables dans ce cas
nullRMSEA(fit)The baseline model's RMSEA = 0.1521099
CFI, TLI, and other incremental fit indices may not be very informative because the baseline model's RMSEA < 0.158 (Kenny, Kaniskan, & McCoach, 2015). donc la validité du modèle sera basée sur les indices RMSEA et SRMR
On peut comparer les résultats avec ceux obtenus en considérant les moyennes des résultats au questionnaire.
fit %>% parameterestimates(standardized = T) %>% filter(label %in% c("a","b","I")) %>% datatable() %>%
formatRound(columns = 5:12,digits=3)On peut calculer les scores des variables latentes (sans considérer les relations du modèle struxcturel) :
LVsc<-lavPredict(fit)ou bien on peut prédire les valeurs des variables \(y\) (observées) en fonction des valeurs des variables \(x\) (observées) dans un modèle d’équation structurelle.
REGsc<-lavPredictY(fit,ynames = paste("RE",1:5,sep=""),
xnames=c(paste("Sec",1:5,sep=""),paste("Eval",1:5,sep=""),paste("Cl",1:4,sep=""))
)Test de l’invariance du modèle de mesure :
Une des grandes forces de la modélisation en SEM est la validation psychométrique de questionnaires. La fonction dédiée est cfa() pour analyse factorielle confirmatoire.
Si on considère qeux populations différentes, l’un des problème lorsque l’on cherche à valider un questionnaire est de savoir si :
La structure factorielle du questionnaire est invariante entre les deux populations (configural invariance), c’est à dire les items sont-ils associés aux même variables latentes dans les deux populations.
En plus de la structure factorielle identique, le poids de la variable latente dans la variabilité des items est-il le même entre les deux populations (weak or metric invariance), c’est à dire peut-on considérer les loadings égaux entre les deux populations ?
On ajoute ensuite la condition suivante : les intercepts des items sont-ils les même dans les deux populations (strong or scalar invariance) ?
Enfin on ajoute la condition sur les erreurs de mesures : les variances et covariance des erreurs de mesure sont elles les mêmes entre les deux populations (stict invariance) ?
Il s’agit donc de tester des modèles emboités, le test de rapport de vraisemblance peut être utilisé mais comme pour la validation du modèle celui-ci est sensible à la non normalité des données on utilise plutôt les indices CFI et RMSEA. La règle \(\Delta CFI<.01, \quad \Delta RMSEA<.01\) est la plus utilisée en pratique (validée par des simulations)
Quelques références :
Intérêt de ces contraintes
L’intérêt de ces questions est de savoir si la différence des variables latentes entre les deux populations est attribuable à une différence réelle ou bien à une différence d’utilisation de l’échelle de mesure.
model<-'
SEP=~SEP1+SEP2+SEP3+SEP4+SEP5
RE=~RE1+RE2+RE3+RE4+RE5
Eval=~Eval1+Eval2+Eval3+Eval4+Eval5
Cl=~Cl1+Cl2+Cl3+Cl4
Sec=~Sec1+Sec2+Sec3+Sec4+Sec5
SEP~ RE
Math~ RE + SEP+Eval
RE~Sec+Cl
Eval~~Sec
Eval~~Cl
Cl~~Sec
'
fit0<-sem(model,data=df,fixed.x=FALSE,estimator="MLR",meanstructure=T)
fit_config<-sem(model,data=df,fixed.x=FALSE,estimator="MLR",group="Genre")
fit_weak<-sem(model,data=df,fixed.x=FALSE,estimator="MLR",group="Genre",group.equal="loadings")
fit_strong<-sem(model,data=df,fixed.x=FALSE,estimator="MLR",group="Genre",group.equal=c("loadings","intercepts"))
fit_strict<-sem(model,data=df,fixed.x=FALSE,estimator="MLR",group="Genre",group.equal=c("loadings","intercepts","residuals"))Pour pouvoir comparer les modèles il faut ajouter le paramètre meanstructure=T dans le modèle initial car les modèles contraints ont cette propriété et ne seront comparables au modèle initial que si celui-ci possède cette même contrainte.
compareFit(fit0,fit_config,fit_weak,fit_strong,fit_strict) %>% summary()################### Nested Model Comparison #########################
Scaled Chi-Squared Difference Test (method = "satorra.bentler.2001")
lavaan NOTE:
The "Chisq" column contains standard test statistics, not the
robust test that should be reported per model. A robust difference
test is a function of two standard (not robust) statistics.
Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
fit0 267 19004 19308 691.06
fit_config 534 18945 19553 1040.13 351.06 267 0.0004160 ***
fit_weak 553 18941 19480 1074.38 27.20 19 0.1001230
fit_strong 573 18950 19416 1123.70 48.68 20 0.0003413 ***
fit_strict 598 18979 19353 1202.06 54.09 25 0.0006463 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
####################### Model Fit Indices ###########################
chisq.scaled df.scaled pvalue.scaled rmsea.robust cfi.robust
fit0 627.785† 267 .000 .072† .798†
fit_config 992.910 534 .000 .079 .751
fit_weak 1018.532 553 .000 .078 .746
fit_strong 1066.758 573 .000 .079 .731
fit_strict 1123.524 598 .000 .081 .709
tli.robust srmr aic bic
fit0 .773† .093† 19003.825 19308.138†
fit_config .721 .102 18944.747 19553.374
fit_weak .724 .107 18940.999† 19479.964
fit_strong .718 .109 18950.316 19415.952
fit_strict .708 .115 18978.676 19352.652
################## Differences in Fit Indices #######################
df.scaled rmsea.robust cfi.robust tli.robust srmr
fit_config - fit0 267 0.007 -0.047 -0.052 0.009
fit_weak - fit_config 19 -0.001 -0.005 0.004 0.005
fit_strong - fit_weak 20 0.001 -0.015 -0.006 0.001
fit_strict - fit_strong 25 0.001 -0.022 -0.010 0.006
aic bic
fit_config - fit0 -59.078 245.236
fit_weak - fit_config -3.747 -73.409
fit_strong - fit_weak 9.316 -64.012
fit_strict - fit_strong 28.361 -63.300Comparaison des modèle de régressions sur les variables latentes (on contraint les loadings à être égaux) On teste par test de rapport de vraisemblance le modèle latent contraint (\(H_0:\) égalité des coefficients de régressions entre les deux populations) contre le modèle latent non contraint.
fit_reg<-sem(model,data=df,fixed.x=FALSE,estimator="MLR",group="Genre",group.equal=c("loadings","regressions"))
lavTestLRT(fit_weak,fit_reg)
Scaled Chi-Squared Difference Test (method = "satorra.bentler.2001")
lavaan NOTE:
The "Chisq" column contains standard test statistics, not the
robust test that should be reported per model. A robust difference
test is a function of two standard (not robust) statistics.
Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
fit_weak 553 18941 19480 1074.4
fit_reg 559 18934 19451 1079.3 4.3498 6 0.6294Exemple de Cross Lagged Model (CLM)
Les données pour cet exemple sont ici
Il s’agit toujours de la même problématique et on ajoute une dimension temporelle dans le modèle :
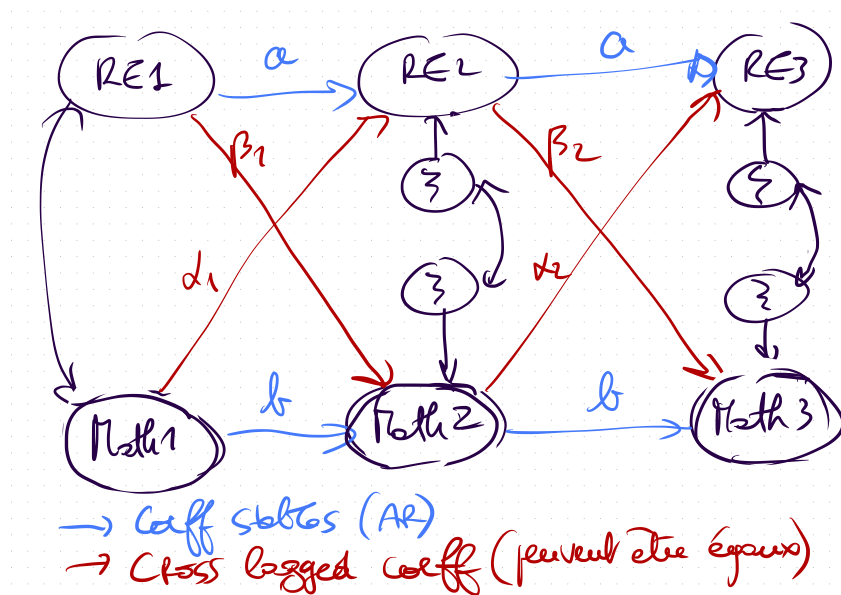
EXERCICE : écrire le modèle précédent en considérant que les coefficients cross-lagged ne sont pas les mêmes entre les deux temps de mesure
Voir la correction
dataLongit<-read.csv("dataLongit.csv")
modelLongit1<-'
## Measurement model
RE1=~RE.1.1+RE.1.2+RE.1.3+RE.1.4+RE.1.5
RE2=~RE.2.1+RE.2.2+RE.2.3+RE.1.4+RE.2.5
RE3=~RE.3.1+RE.3.2+RE.3.3+RE.3.4+RE.3.5
## Covariance
RE1~~Math1
RE2~~Math2
RE3~~Math3
## Regressions
Math2~b*Math1+RE1
Math3~b*Math2+RE2
RE2~Math1+a*RE1
RE3~Math2+a*RE2
'
fit1<-sem(modelLongit1,data=dataLongit,estimator="MLR")Spécifier un modèle avec des coefficients cross-lagged constants.
Voir la correction
modelLongit2<-'
## Measurement model
RE1=~RE.1.1+RE.1.2+RE.1.3+RE.1.4+RE.1.5
RE2=~RE.2.1+RE.2.2+RE.2.3+RE.1.4+RE.2.5
RE3=~RE.3.1+RE.3.2+RE.3.3+RE.3.4+RE.3.5
## Covariance
RE1~~Math1
RE2~~Math2
RE3~~Math3
## Regressions
Math2~b*Math1+c*RE1
Math3~b*Math2+c*RE2
RE2~d*Math1+a*RE1
RE3~d*Math2+a*RE2
'
library(lavaan)
fit2<-sem(modelLongit2,data=dataLongit,estimator="MLR")On peut alors tester si le modèle contraint est statistiquement meilleur que le modèle non contraint.
Voir la correction
lavTestLRT(fit1,fit2)
Scaled Chi-Squared Difference Test (method = "satorra.bentler.2001")
lavaan NOTE:
The "Chisq" column contains standard test statistics, not the
robust test that should be reported per model. A robust difference
test is a function of two standard (not robust) statistics.
Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
fit1 112 13317 13468 353.14
fit2 114 13316 13460 356.27 1.7496 2 0.4169