The COVID-19 wave?
Titre complet
The COVID-19 wave? A longitudinal study of affective experience and coping strategies during the first lockdown in France Galharret J.-M., Sapin A., Bret A., Boudoukha A.-H., Navarro O., Fleury-Bahi G., & Congard A. (Nantes Université)
Les données
Les données correspondent aux affects positifs à faible activation (API) mesurées 12 fois elles sont disponibles ici. Les participants déplacent le curseur sur [0,100] pour donner une évaluation subjective de leur niveau de tranquilité et de .

Voici un extrait des réponses obtenues
## API_t1 API_t2 API_t3 API_t4 API_t5 API_t6 API_t7 API_t8 API_t9 API_t10
## 1 52.5 44.0 42.5 46.5 46.5 47.0 41.0 39.5 43.0 51.5
## 2 18.0 21.5 39.0 24.5 16.0 29.0 26.0 32.0 33.0 45.0
## 3 75.0 70.0 45.0 77.5 74.5 77.0 75.0 36.5 69.0 54.0
## 4 65.0 76.0 89.0 67.0 69.5 73.0 70.0 64.5 65.0 81.0
## 5 49.0 66.0 64.0 63.5 65.5 62.5 68.0 60.0 59.0 67.0
## 6 69.0 87.0 81.0 96.5 83.5 93.0 91.5 79.5 96.5 100.0
## API_t11 API_t12
## 1 61.0 60.0
## 2 69.5 72.5
## 3 53.5 52.5
## 4 77.5 84.5
## 5 69.5 73.5
## 6 97.0 90.0On a \(i=\) 179 participants et \(t=\) 12 temps de mesure.
La modélisation : Trajectoire cubique
On veut estimer les trajectoires temporelles pour chaque individu \(i\) :
\[Y_i(t)=b_{0,i}+b_{1,i} t+ b_{2,i} t^2+ b_{3,i} t^3+\varepsilon_i(t)\]
Problème de colinéarité dans les modèles de trajectoire :
L’estimation par MCO est instable lorsque les variables explicatives sont colinéaires et dans les modèles de trajectoire c’est le cas :
t<-1:12
Xt<-cbind(1,t,t^2,t^3)
# VIF de t^3 en fonction de t et de t^2
1/(1-summary(lm(Xt[,4]~Xt[,2]+Xt[,3]))$r.squared)
## [1] 315.2346\(\leadsto\) Solution : polynomes orthogonaux
Polynômes orthogonaux
On veut déterminer des polynômes \(P_k\) de degré \(k\) qui sont orthogonaux (donc non corrélés) pour \(t=\{1,...,12\}\).
Sur R
X1t<-poly(1:12,3)
par(mfrow=c(1,3))
plot(t,X1t[,1],main="degré 1",type="l")
plot(t,X1t[,2],main="degré 2",type="l")
plot(t,X1t[,3],main="degré 3",type="l")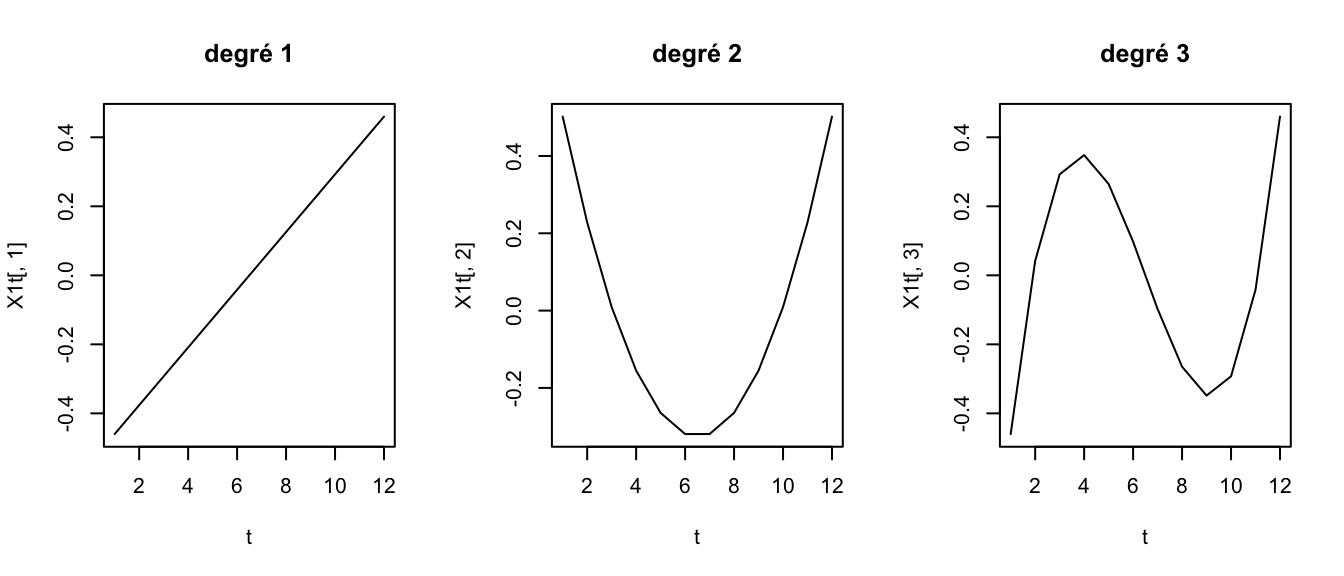
X1t<-cbind(1,X1t)Estimation MCO
On veut estimer \(Y_i(t)=\beta_{0,i}+\beta_{1,i} P_1(t)+ \beta_{2,i} P_2(t)+ \beta_{3,i} P_3(t)+\varepsilon_i(t).\)
Y1<-as.numeric(Y[1,])
mod1<-lm(Y1~X1t[,1]+X1t[,2]+X1t[,3])
Yp<-predict(mod1,interval="prediction")
## Warning in predict.lm(mod1, interval = "prediction"): predictions on current data refer to _future_ responses
plot(t,Y1,pch=20,main="Trajectoire pour l'individu 1",ylim=c(10,80))
lines(t,Yp[,1],col=2)
lines(t,Yp[,2],col=2,lty=2)
lines(t,Yp[,3],col=2,lty=2)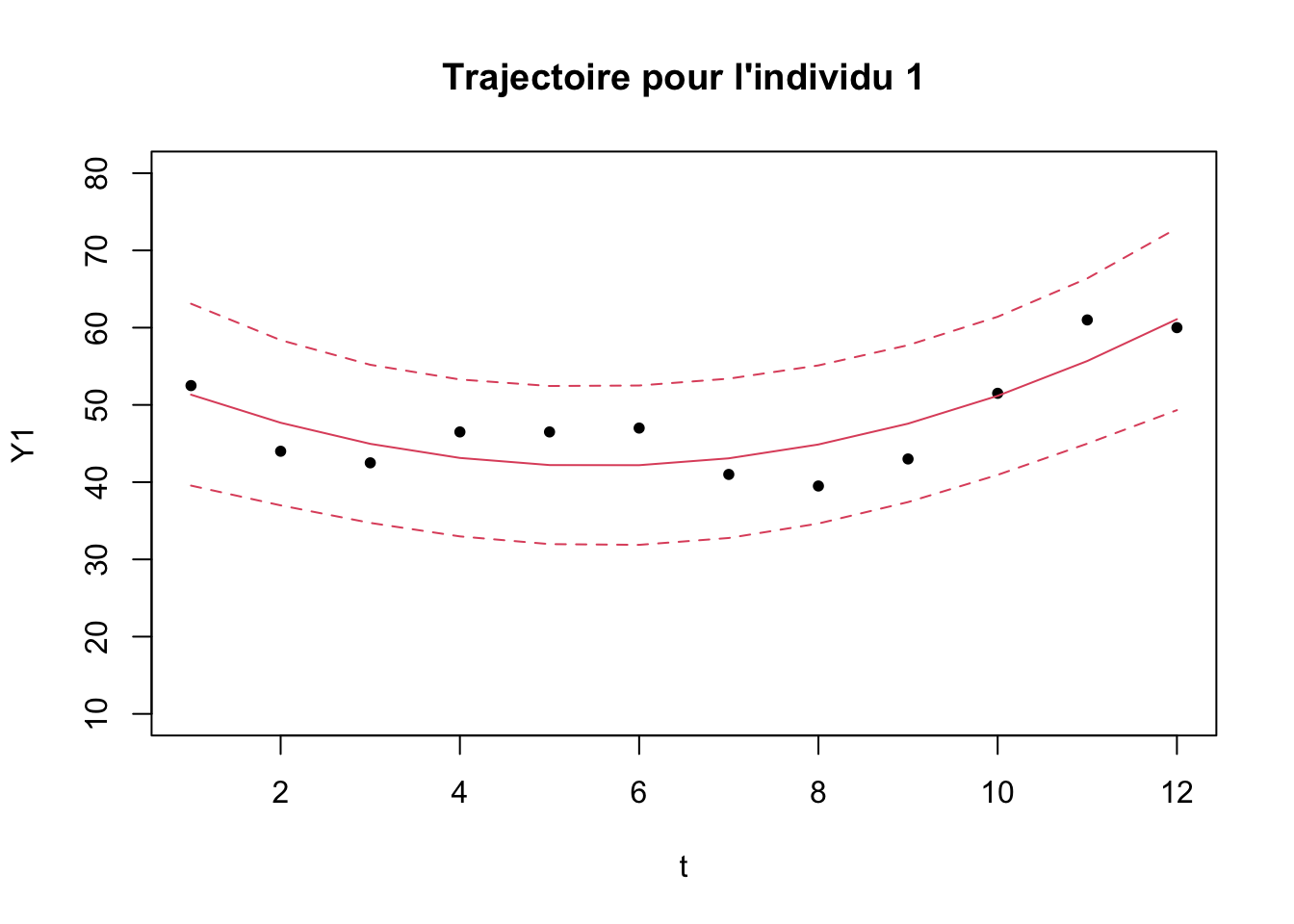
Le modèle bayésien sur Stan
Soit \(\mathbb X=[1,P_1(t),...,P_k(t)]\in \mathbb R^{n \times (k+1)}\) la matrice de design du modèle linéaire on veut estimer \(\beta_{i},\mu,\sigma \in \mathbb R^{k+1}\) et \(\sigma_g \in \mathbb R\) tels que :
- \(Y_{i,t}=\mathbb X \beta_i+\sigma_g \ \varepsilon_i\) où \(\varepsilon_i\sim \mathcal N(0,1)\)
- \(\beta_i=\mu+\sigma \ \varepsilon\) où \(\varepsilon \sim \mathcal N(0,I_{k+1}).\)
model<-'
data{
int <lower=1> n;
// Number of time-measurement
int <lower=1> T;
// degree of the polynom
int<lower=1> k;
// dependant variable
matrix [n,T] y;
// design matrix
matrix [T,k+1] X;
}
parameters {
matrix[n,k+1] beta;
vector[k+1] mu;
vector<lower=0>[k+1] sigma;
real<lower=0> sig;
}
model {
for(t in 1:T){
for (i in 1:n){
y[i,t]~normal(X[t,]*to_vector(beta[i,]),sig);}
}
sig~inv_gamma(.001,.001);
for(j in 1:(k+1)) beta[,j]~normal(mu[j],sigma[j]);
mu~normal(0,100);
sigma~inv_gamma(.001,.001);
}
'Code pour faire tourner le modèle :
library(rstan)
long_model<- stan_model(model_code=model)
fit <- sampling(long_model,data=list(n=dim(Y)[1],T=12,X=X1t,y=Y,p=3), iter = 10000, chains = 2)Les résultats sont disponibles dans le fichier res_bay.RData
On peut regarder les sorties :
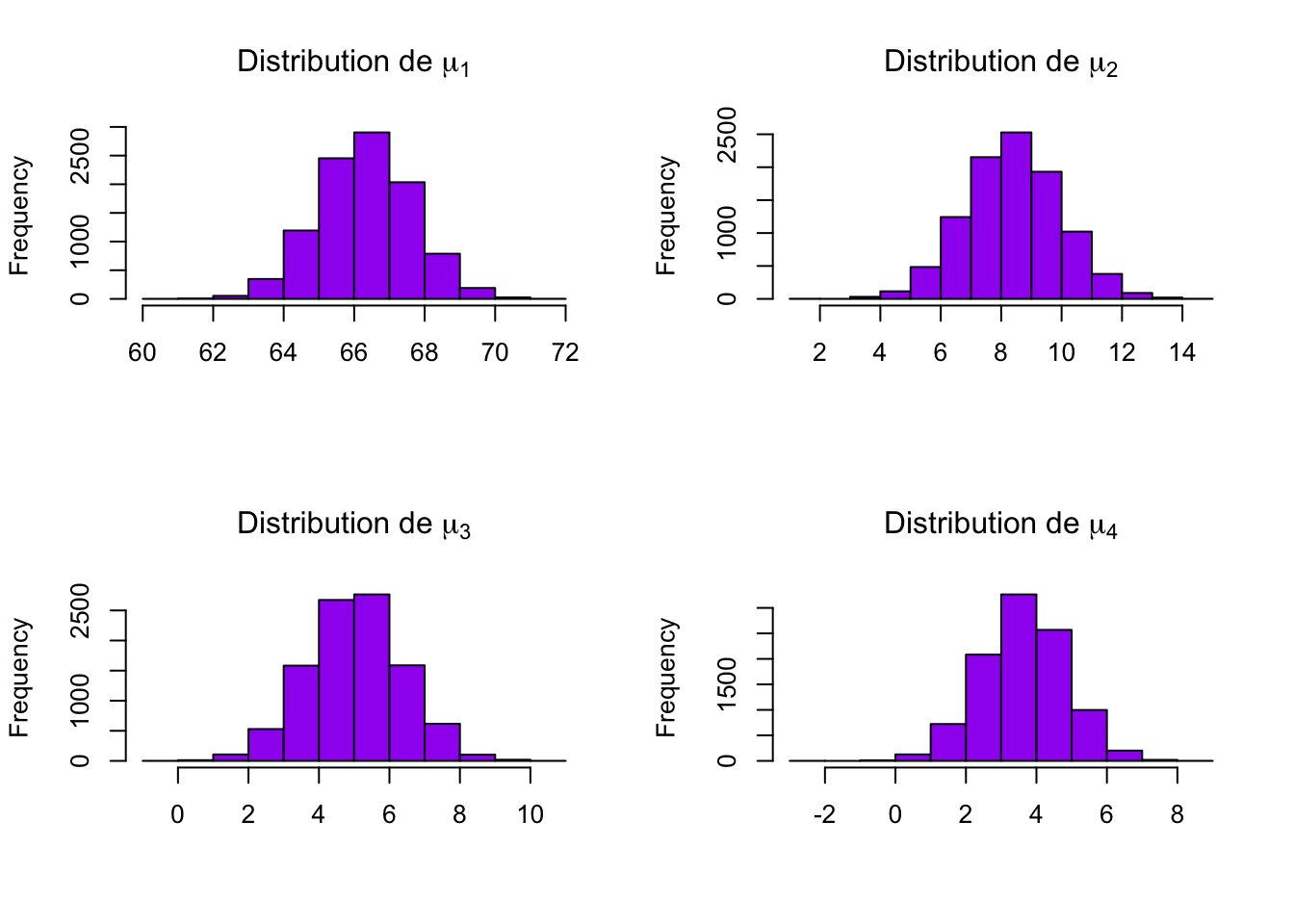
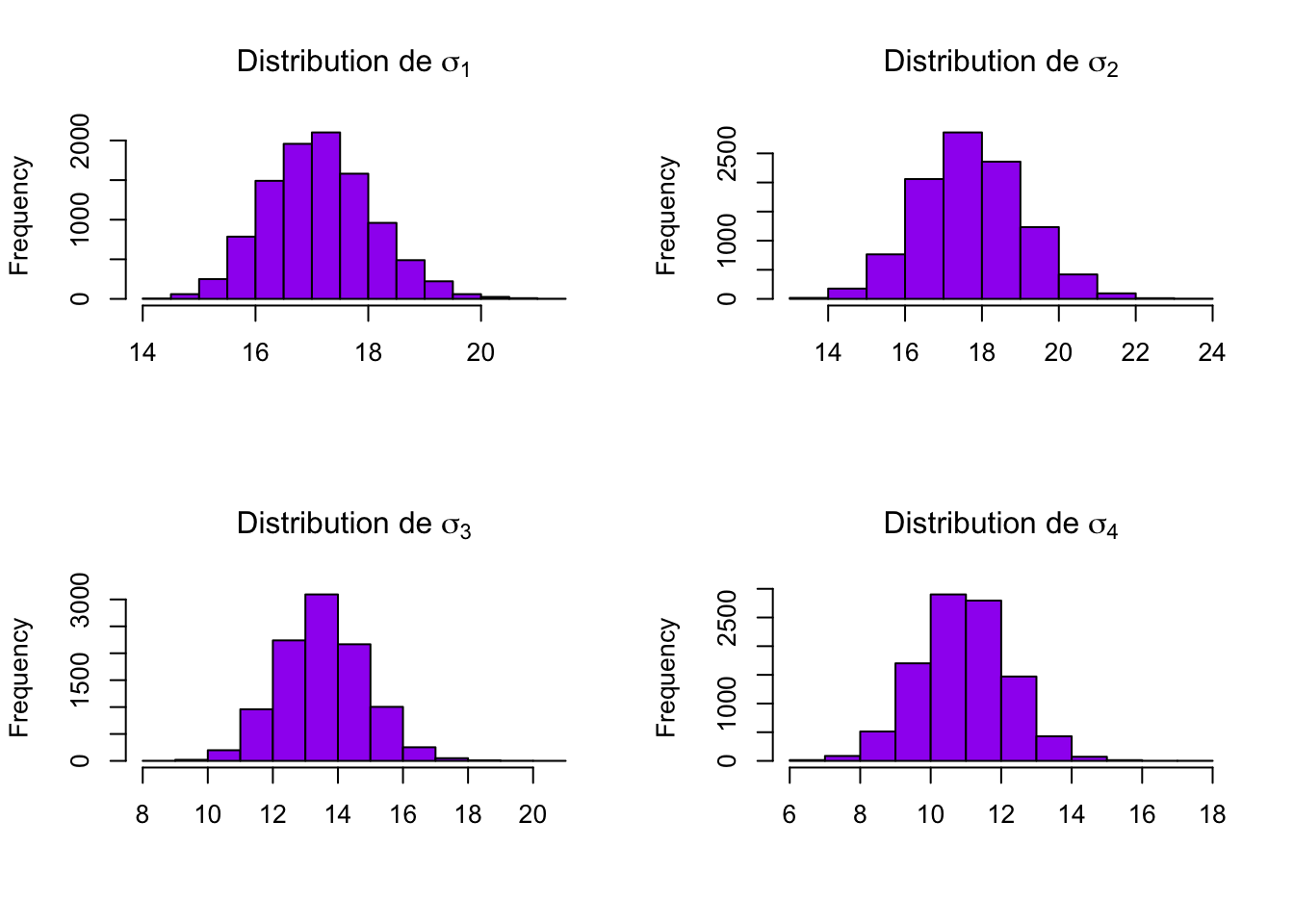
Comparaison bayésien / MCO :
On peut regarder la différence entre l’estimateur MCO et l’estimateur bayésien pour le premier individu.
Ypred<-X1t %*% t(res$beta[1:dim(res$beta)[1],1,])
YpBay<-apply(Ypred,1,mean)
mod1<-lm(Y1~X1t[,1]+X1t[,2]+X1t[,3])
YpMCO<-predict(mod1)
plot(1:12,Y1,pch=20,main="Comparaison des estimateurs pour l'individu 1")
lines(1:12,YpMCO,col=2)
lines(1:12,YpBay,col=3)
legend("bottomright",lty=c(1,1),col=2:3,legend=c("MCO","Bay"),cex=0.75)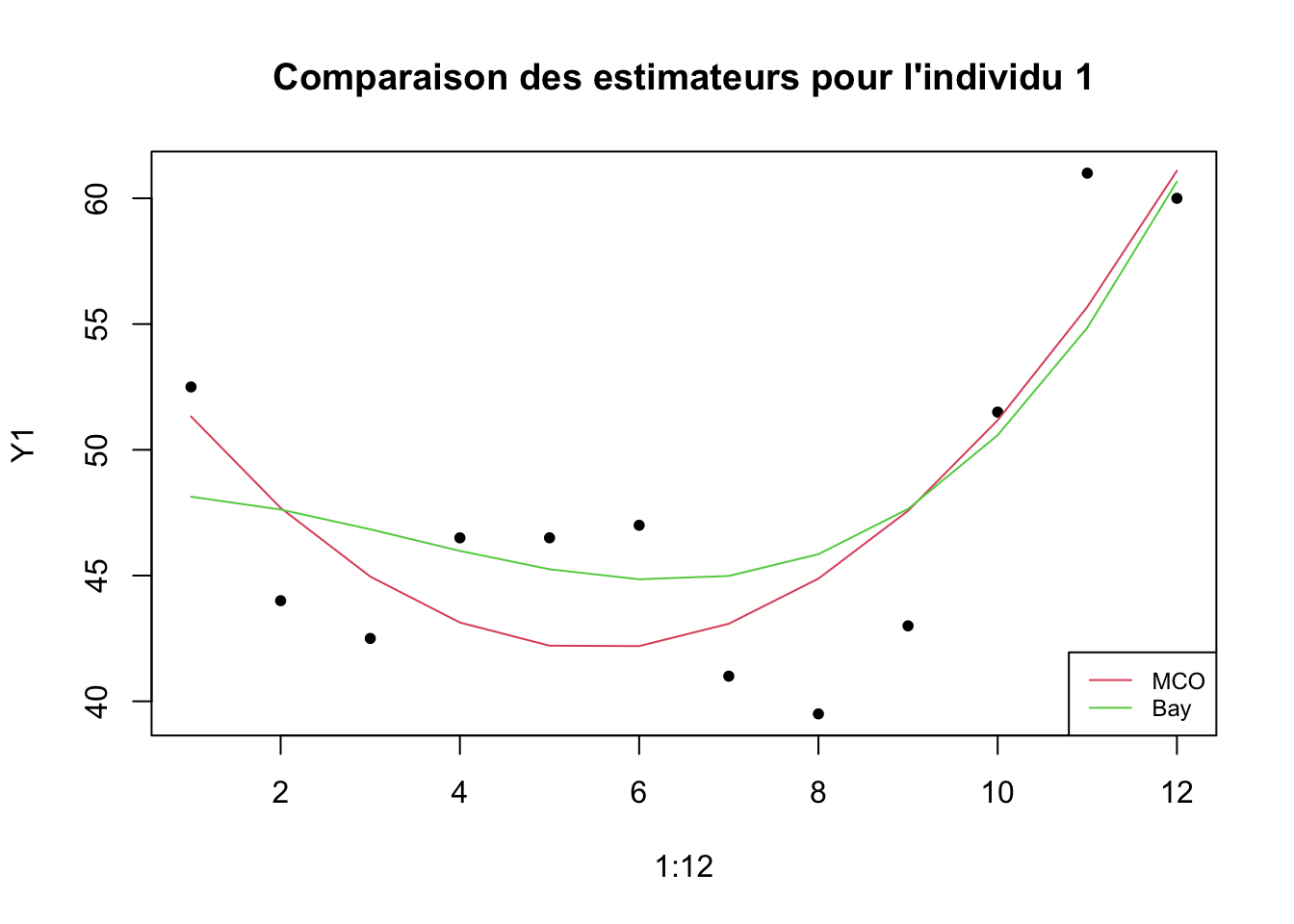
On peut aussi regarder ce que ça donne sur l’individu “moyen”.
n<-dim(Y)[1]
B<-apply(res$mu,2,mean)
dim(X1t)
## [1] 12 4
dim(res$mu)
## [1] 10000 4
Ypred<-X1t %*% t(res$mu)
YpBay<-apply(Ypred,1,mean)
Ym<-apply(Y,2,mean)
mod1<-lm(Ym~X1t[,1]+X1t[,2]+X1t[,3])
YpMCO<-predict(mod1)
plot(1:12,Ym,pch=20,main="Comparaison des estimateurs pour l'individu moyen")
lines(1:12,YpMCO,col=2)
lines(1:12,YpBay,col=3)
legend("bottomright",lty=c(1,1),col=2:3,legend=c("MCO","Bay"),cex=0.75)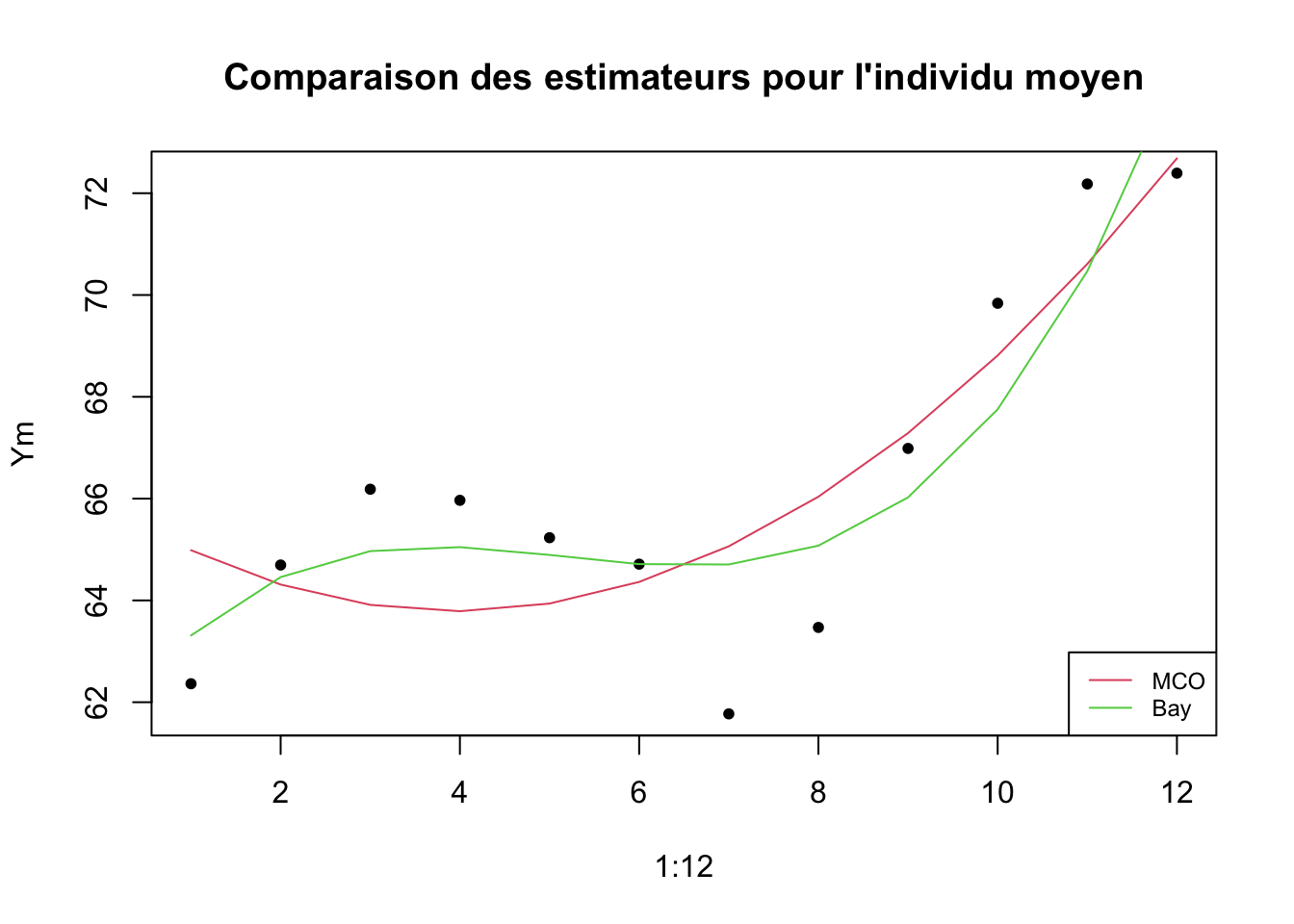
Etude des trajectoires individuelles :
On va considérer deux cas :
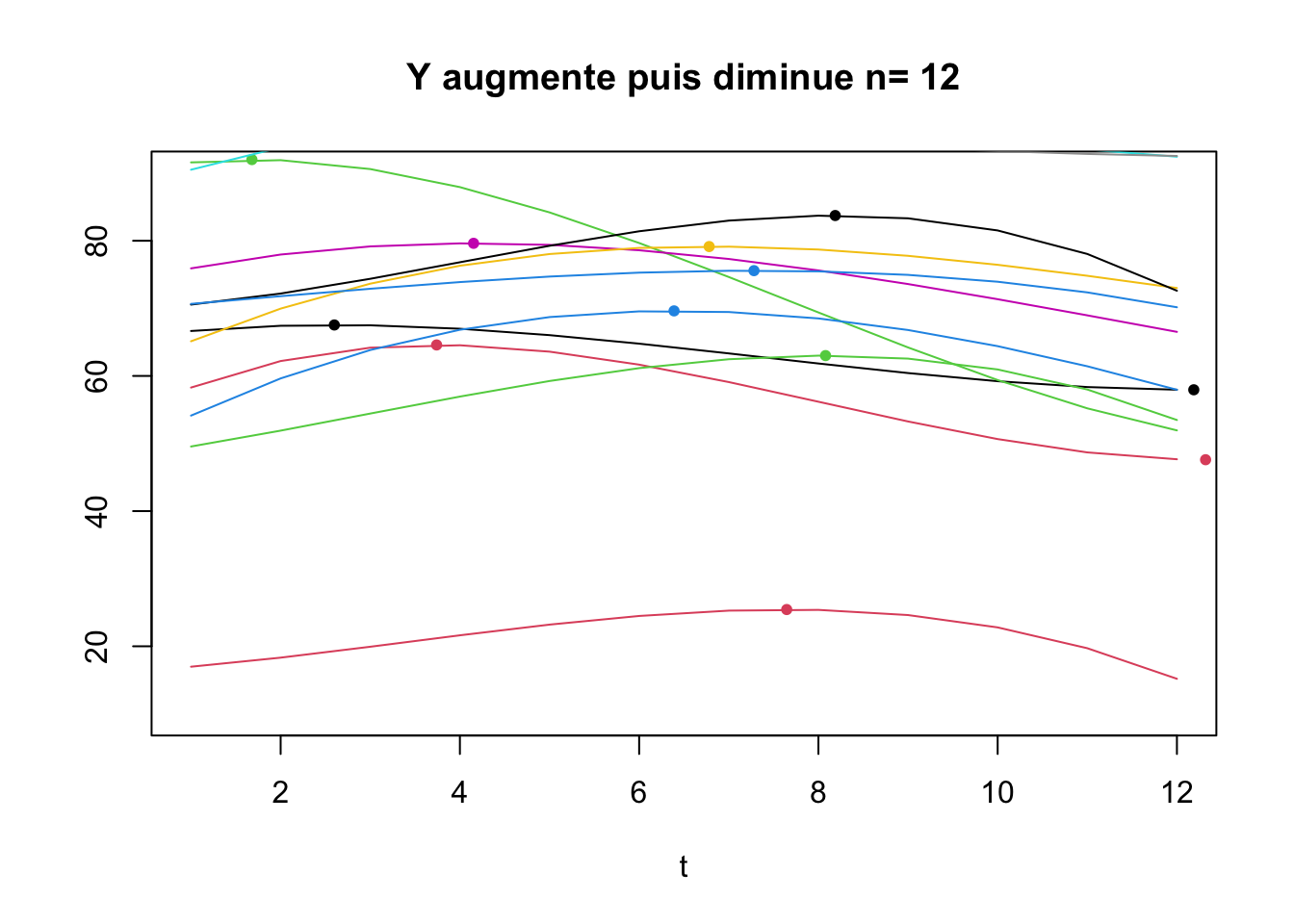
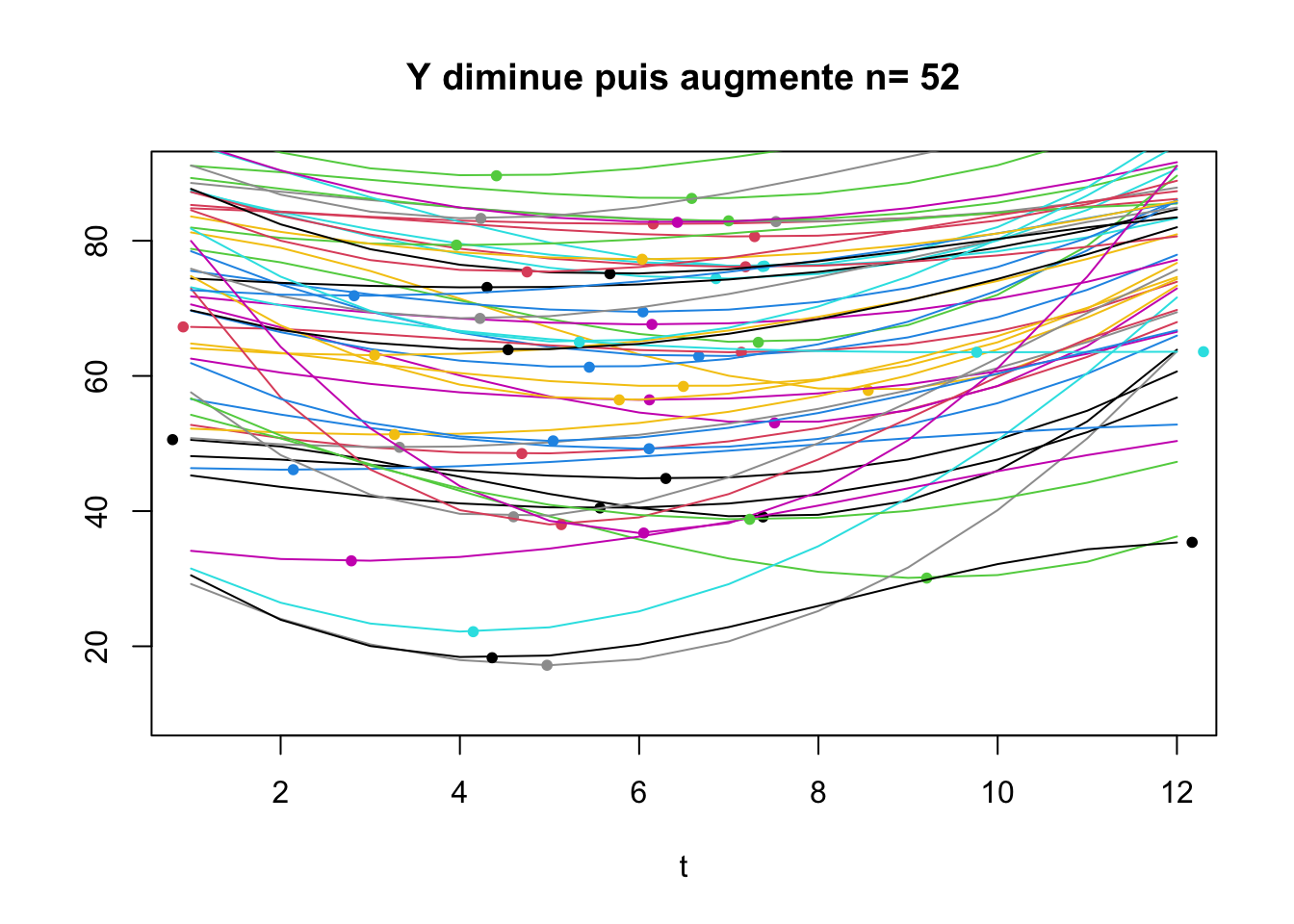
Les individus pour lequels \(Y\) change de direction sur l’intervalle d’étude (i.e. Y augmente puis diminue puis réaugmente)
Les individus pour lequels \(Y\) ne change pas de direction sur l’intervalle d’étude mais pour lesquels il existe un point d’inflexion dans l’intervalle.
La majorité des Individus connaît deux changements de direction
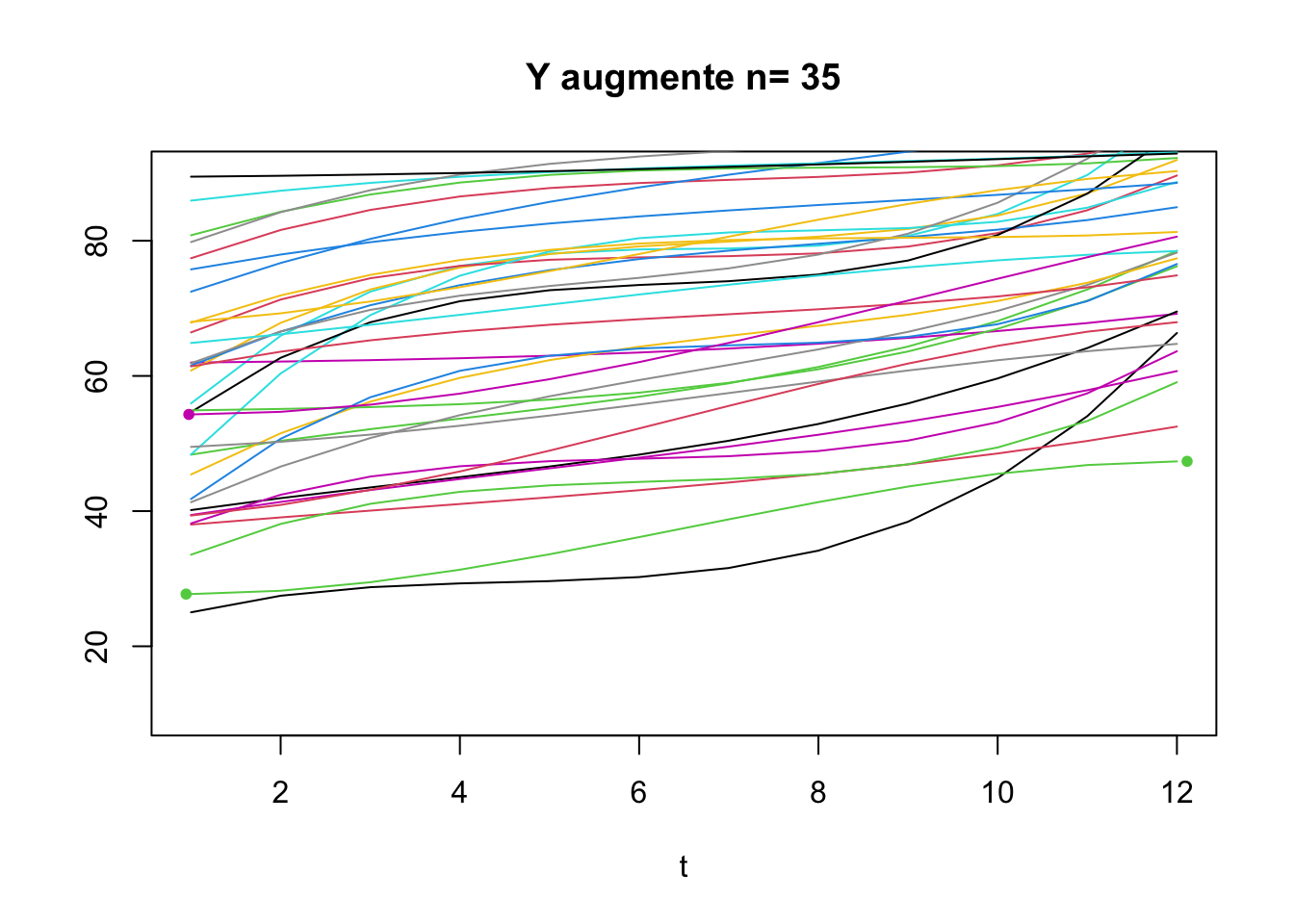
80 individus ont deux changements de direction, 64 un seul et 35 ont des affects qui ne font qu’augmenter.
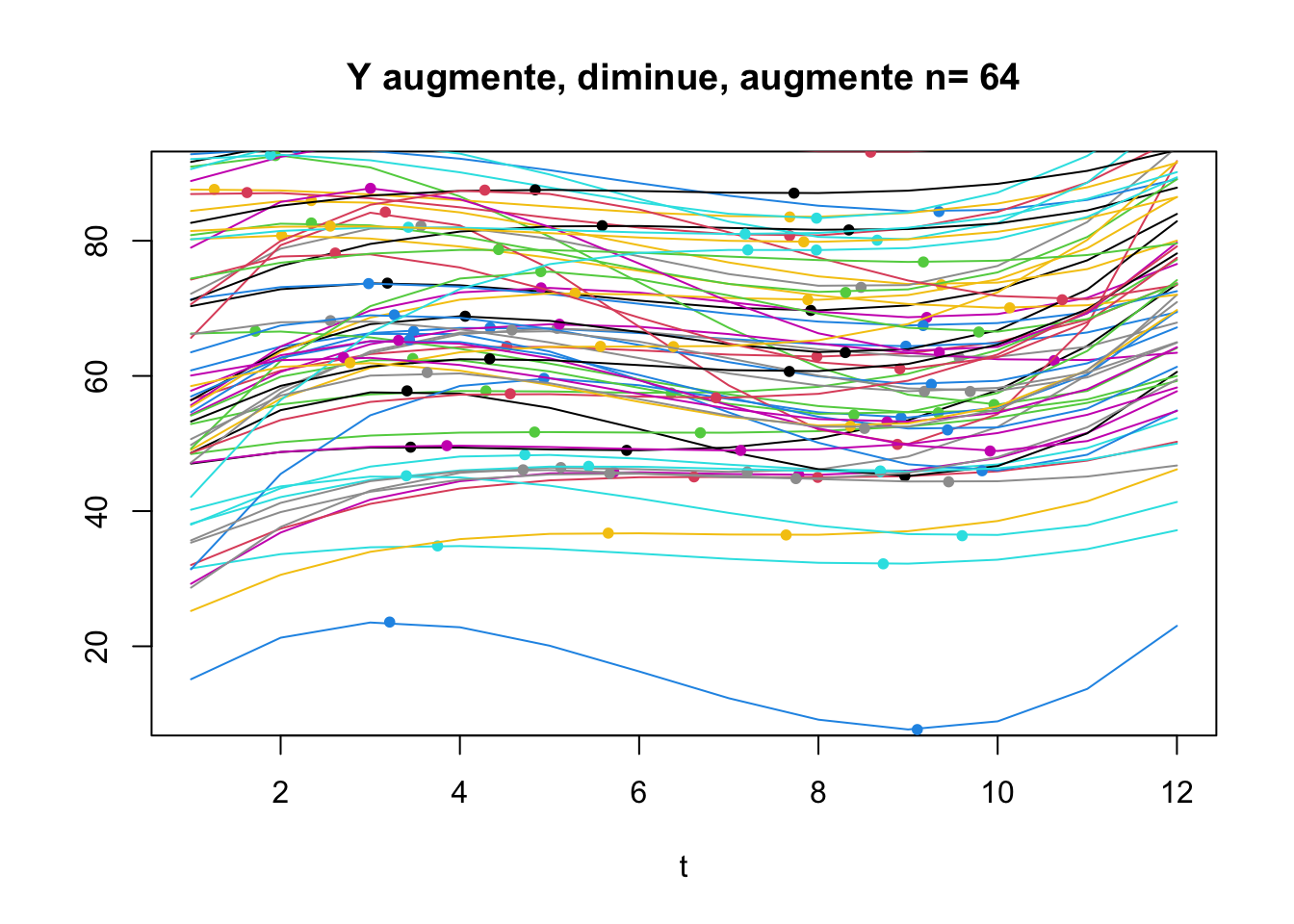
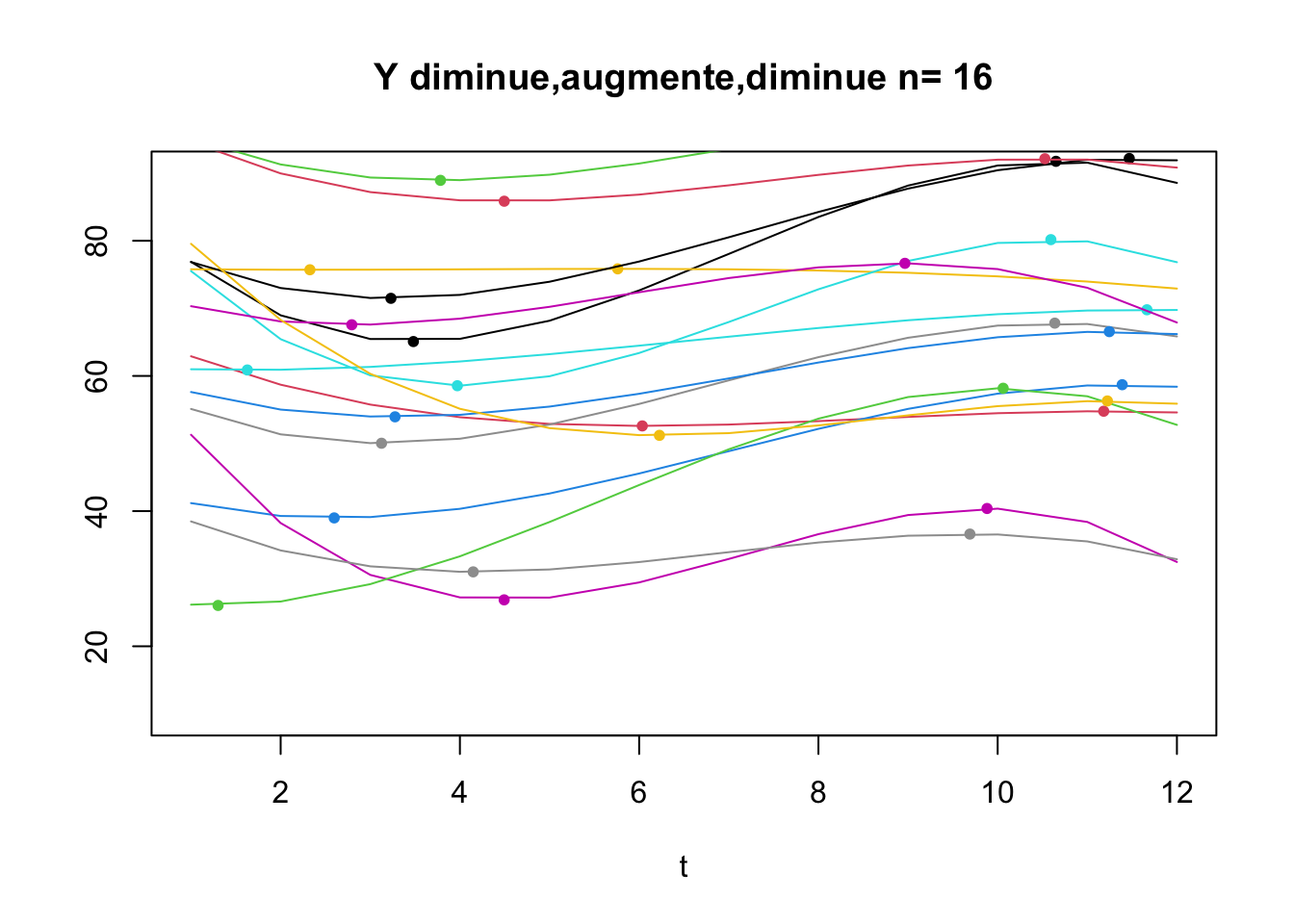
Qu’est-ce qu’un point d’inflexion?
Pour \(Y\) polynôme de degré 3, il s’agit du point (unique) \(t_0\) tel que \(Y''(t_0)=0.\)
Lorsque \(t_0\) est un point d’inflexion du polynôme de dégré 3 la tangente en \(t_0\) traverse la courbe.
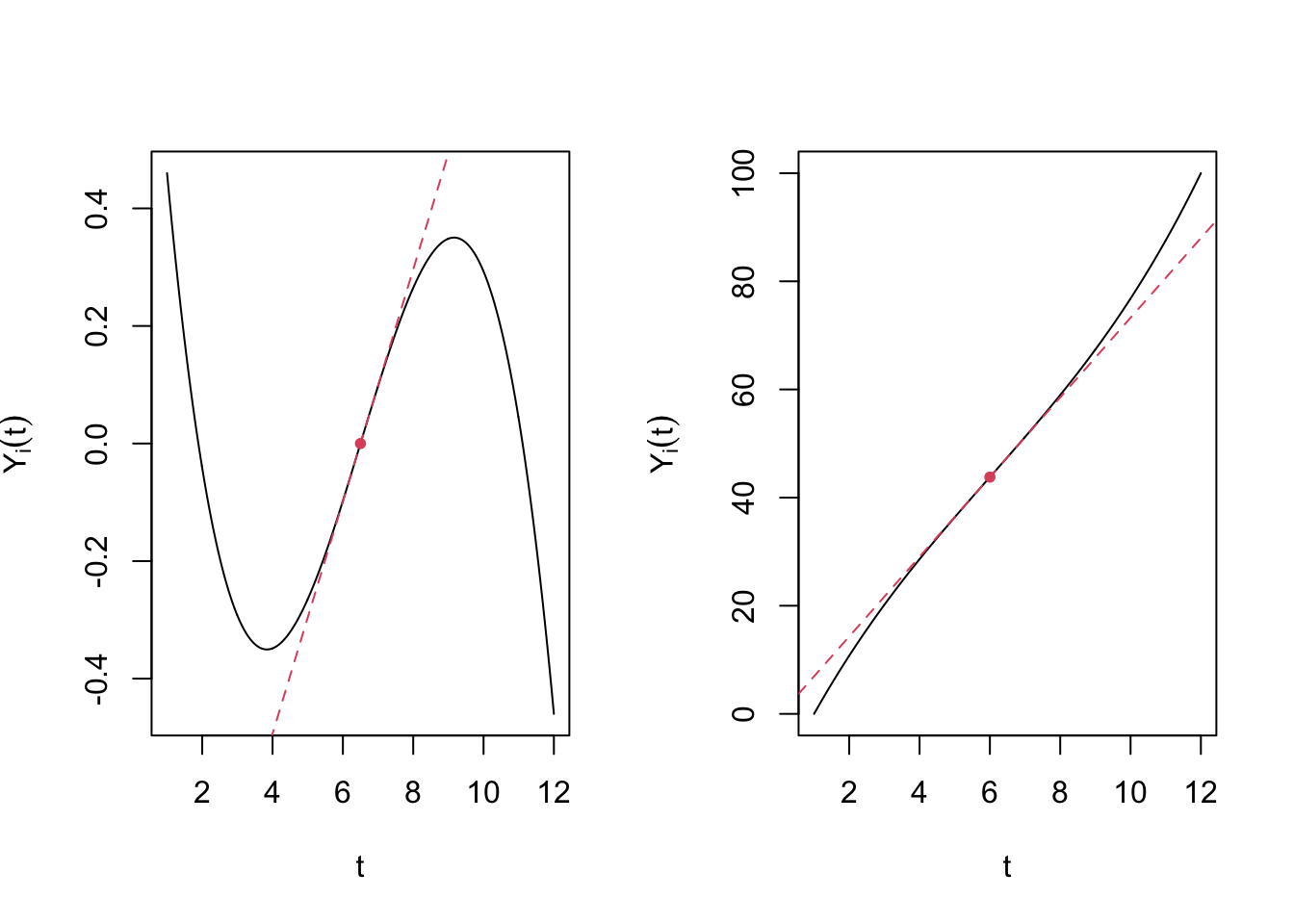
- Lorsque le coefficient de \(t^3\) est positif soit l’augmentation de \(Y\) accélère jusqu’à \(t_0\) puis ralentit (graphe de gauche) ou bien le contraire (graphe de droite).
Les points d’inflexion pour l’affect considéré
On constate que pour la plupart des participants le point d’inflexion est situé entre la semaine 4 et la semaine 8 (surtout pour les 73 individus identifiés précédemment).
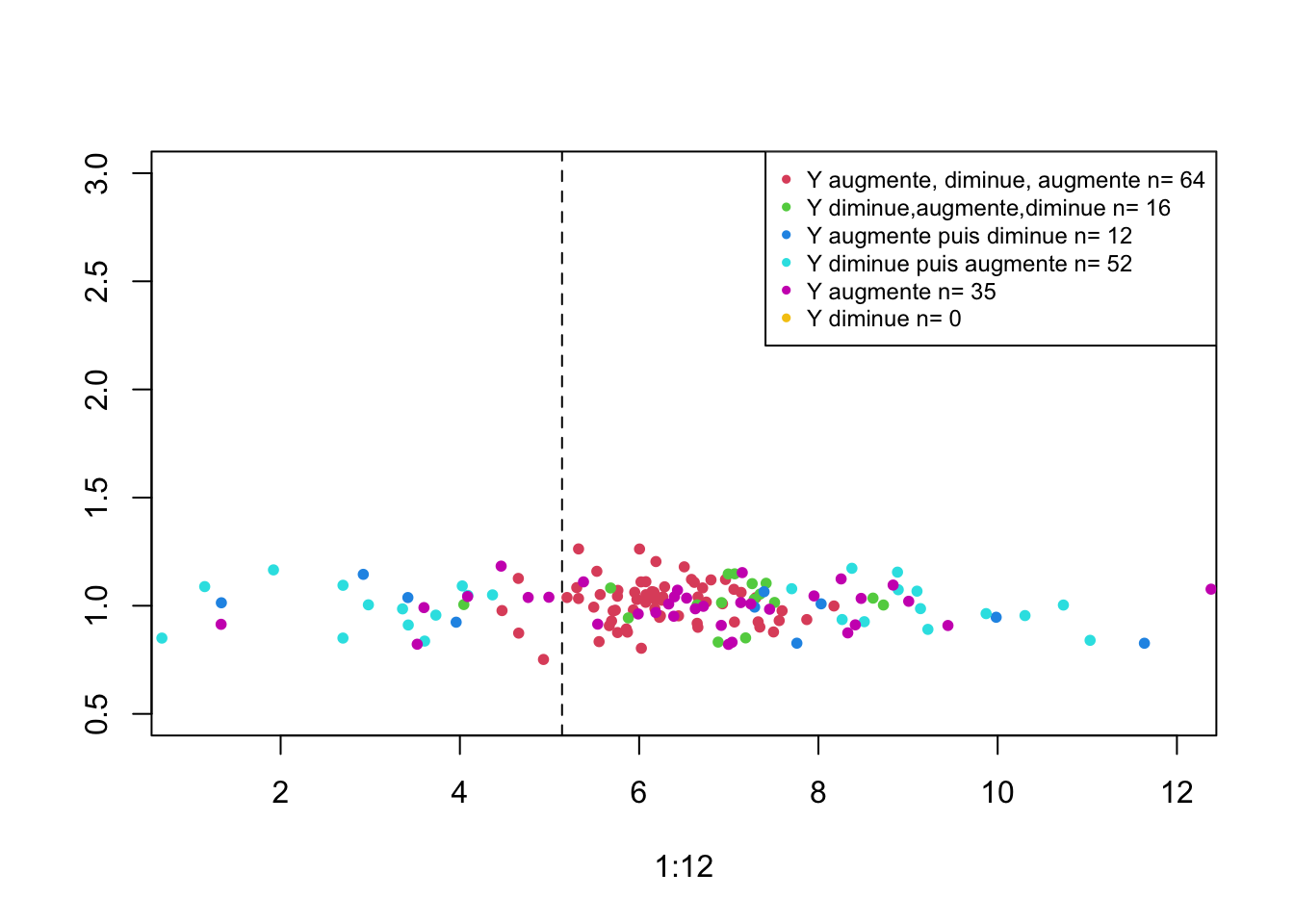
On constate que pour la plupart des participants le point d’inflexion est situé entre la semaine 4 et la semaine 8. La moyenne étant 5.1397187.
B<-dim(res_bay[[1]]$beta)[1]
P_API<-rep(NA,n)
P_APA<-rep(NA,n)
P_ANI<-rep(NA,n)
P_ANA<-rep(NA,n)
for(i in 1:n){
P_API[i]<-inflex_coord(coef_t(apply(res_bay[[1]]$beta[1:B,i,],2,mean)))[1]
P_APA[i]<-inflex_coord(coef_t(apply(res_bay[[2]]$beta[1:B,i,],2,mean)))[1]
P_ANI[i]<-inflex_coord(coef_t(apply(res_bay[[3]]$beta[1:B,i,],2,mean)))[1]
P_ANA[i]<-inflex_coord(coef_t(apply(res_bay[[4]]$beta[1:B,i,],2,mean)))[1]
}
boxplot(cbind(P_API,P_APA,P_ANA,P_ANI),ylim=c(1,12))
abline(h=c(inflex_coord(coef_t(apply(res_bay[[1]]$mu,2,mean)))[1],
inflex_coord(coef_t(apply(res_bay[[2]]$mu,2,mean)))[1],
inflex_coord(coef_t(apply(res_bay[[3]]$mu,2,mean)))[1],
inflex_coord(coef_t(apply(res_bay[[4]]$mu,2,mean)))[1]))